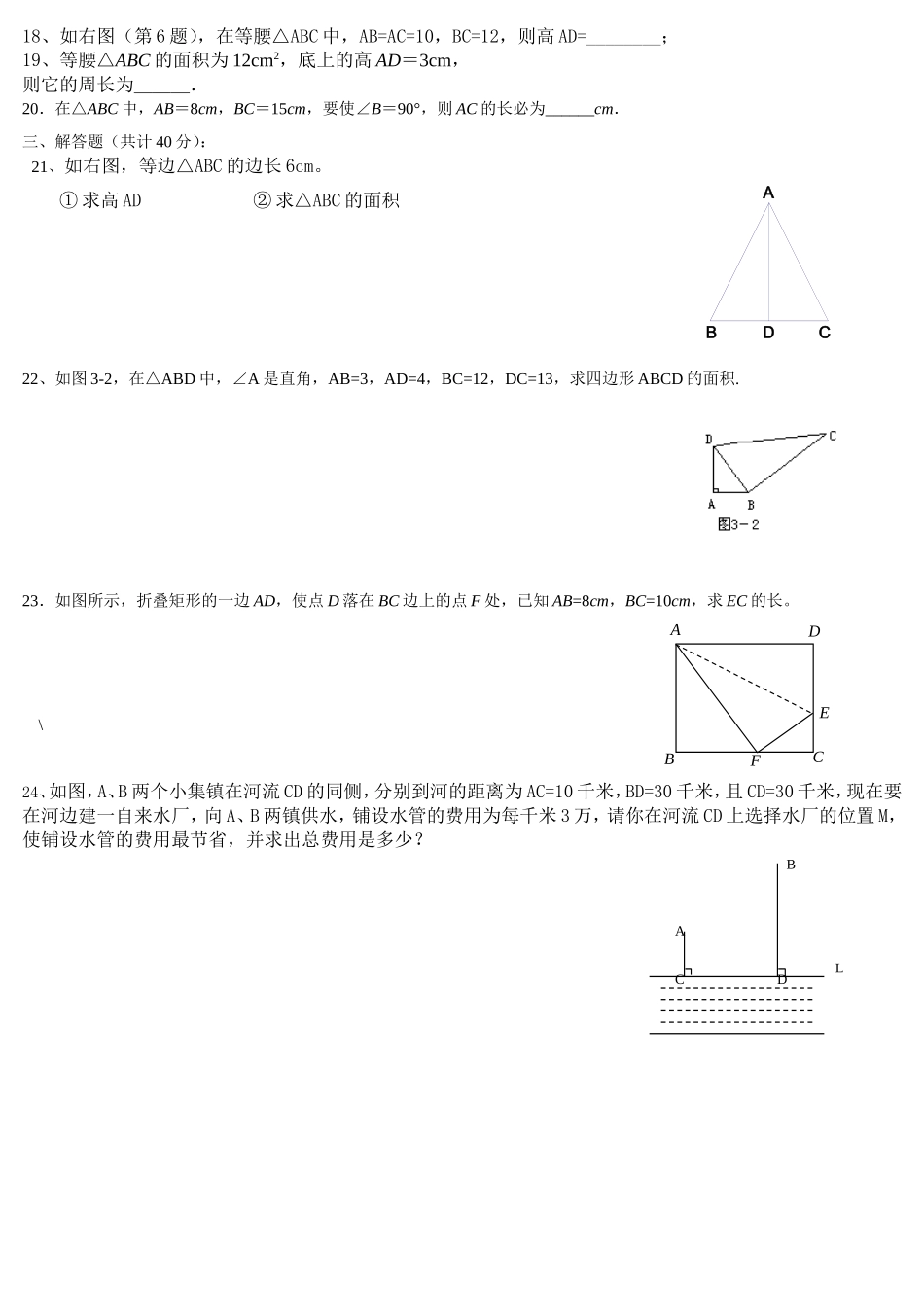
(第6题)ABDC《勾股定理》单元复习试题(一)一、选择题(每小题3分):1.如果梯子的底端离建筑物5米,13米长的梯子可以达到建筑物的高度是()A.12米B.13米C.14米D.15米2.分别以下列五组数为一个三角形的边长:①6,8,10;②13,5,12③1,2,3;④9,40,41;⑤3,4,5.其中能构成直角三角形的有()组A.2B.3C.4D.53.在△ABC中,∠C=90°,周长为60,斜边与一直角边比是13∶5,则这个三角形三边长分别是()A.5,4,3B.13,12,5C.10,8,6D.26,24,104.在△ABC中,已知AB=12cm,AC=9cm,BC=15cm,则△ABC的面积等于()A.108cm2B.90cm2C.180cm2D.54cm25.在直角坐标系中,点P(2,3)到原点的距离是()A.B.C.D.26.在△ABC中,∠A=90°,∠A、∠B、∠C的对边长分别为a、b、c,则下列结论错误的是()A.a2+b2=c2B.b2+c2=a2C.D.7.如图1,2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的《勾股圆方图》(也称《赵爽弦图》),它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,如果大正方形的面积是13,小正方形式面积是1,直角三角形的短直角边为a,较长直角边为b,那么的值为()A.13B.19C.25D.1698.如图2,分别以直角△ABC的三边AB,BC,CA为直径向外作半圆.设直线AB左边阴影部分的面积为S1,右边阴影部分的面积和为S2,则()A.S1=S2B.S1<S2C.S1>S2D.无法确定9.如图3所示,AB=BC=CD=DE=1,AB⊥BC,AC⊥CD,AD⊥DE,则AE=()A.1B.C.D.210.直角三角形有一条直角边长为13,另外两条边长是连续自然数,则周长为()A.182B.183C.184D.185二、填空题(每小题3分):11.一直角三角形的两边长分别为5和12,则第三边的长是。12.直角三角形两直角边长分别为5和12,则它斜边上的高为_______.13.直角三角形的三边长为连续偶数,则这三个数分别为__________.14.如图5,一根树在离地面9米处断裂,树的顶部落在离底部12米处.树折断之前有____米.15.如果一个三角形的三个内角之比是1∶2∶3,且最小边的长度是8,最长边的长度是______.16、若三角形三条边的长分别为7,24,25,则这个三角形的最大内角是度.17、在△ABC中,∠C=90°,若c=10,a∶b=3∶4,则ab=.图5ABC图2图1图3ABCDEABDC18、如右图(第6题),在等腰△ABC中,AB=AC=10,BC=12,则高AD=________;19、等腰△ABC的面积为12cm2,底上的高AD=3cm,则它的周长为___.20.在△ABC中,AB=8cm,BC=15cm,要使∠B=90°,则AC的长必为______cm.三、解答题(共计40分):21、如右图,等边△ABC的边长6cm。①求高AD②求△ABC的面积22、如图3-2,在△ABD中,∠A是直角,AB=3,AD=4,BC=12,DC=13,求四边形ABCD的面积.23.如图所示,折叠矩形的一边AD,使点D落在BC边上的点F处,已知AB=8cm,BC=10cm,求EC的长。\24、如图,A、B两个小集镇在河流CD的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A、B两镇供水,铺设水管的费用为每千米3万,请你在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少?ABCFEDABCDL