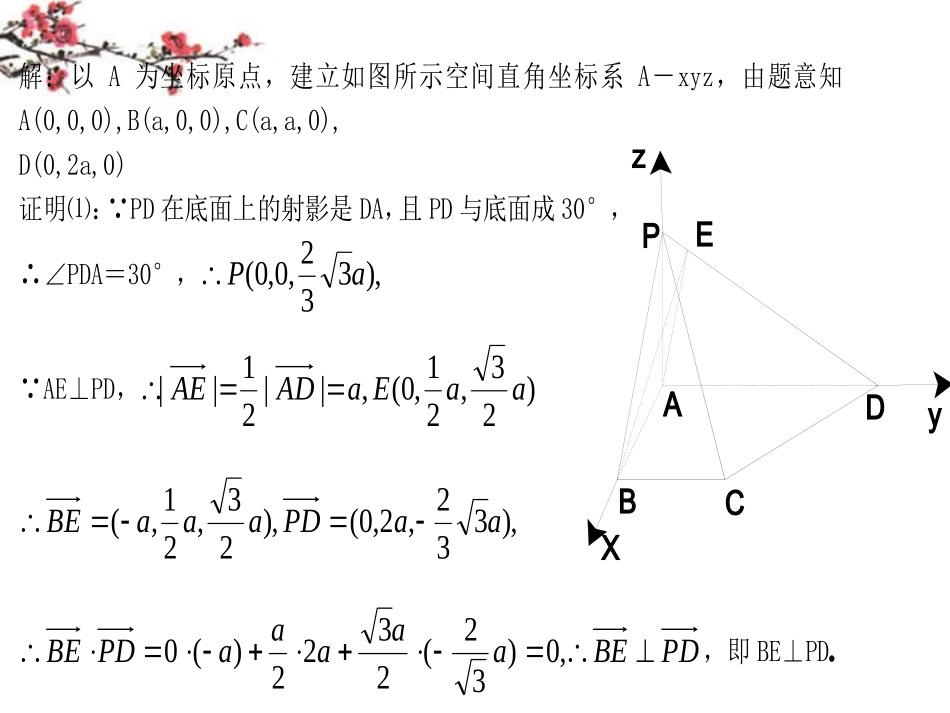
方法总结⒈解立体几何问题的基本思路:化立体几何问题为平面几何问题.⒉熟练掌握所学习的定义、定理,掌握空间直线与直线、直线与平面、平面与平面的相互位置关系的内在联系,灵活的进行互相转化是解立体几何证明题的基础.⒊关于空间的角和距离的计算问题,要依据定义转化为平面概念,然后灵活运用勾股定理、正余弦定理和向量方法进行计算.要严格按照“一作、二证、三计算”,即先构造、再定性、后定量的程序进行.⒋空间向量是解决立体几何问题的有力工具.要熟练掌握向量的各种运算的定义、几何意义,恰当的引入向量运算,化几何证明、逻辑推理为简单的代数运算,以降低解题难度.角和距离求空间的角和距离一、例题例1在四棱锥P-ABCD中,底面ABCD是一直角梯形,∠BAD=90°,AD∥BC,AB=BC=a,AD=2a,且PA⊥底面ABCD,PD与底面成30°(PD和其在底面上的射影所成的角)奎屯王新敞新疆⑴若AE⊥PD,垂足为E,求证:BE⊥PD;⑵求异面直线AE与CD所成角的大小奎屯王新敞新疆____E_P_D_C_B_AzyXEPDCBA解:以A为坐标原点,建立如图所示空间直角坐标系A-xyz,由题意知A(0,0,0),B(a,0,0),C(a,a,0),D(0,2a,0)证明⑴: PD在底面上的射影是DA,且PD与底面成30°,∴∠PDA=30°,),332,0,0(aP AE⊥PD,)23,21,0(,||21||aaEaADAE),332,2,0(),23,21,(aaPDaaaBEPDBEaaaaaPDBE,0)32(2322)(0,即BE⊥PD奎屯王新敞新疆解⑵:由⑴知,2),0,,(),23,2,0(2aCDAEaaCDaaAE又42||||,cos,2||,||CDAECDAECDAEaCDaAE,∴异面直线AE与CD所成角的大小为arccos.42OQPDCBASz例2.如图,正四棱锥SABCD中,所有棱长都是2,P为SA的中点,(1)求二面角BSCD的大小;(2)如果点Q在棱SC上,那么直线BQ与PD能否垂直?请说明理由奎屯王新敞新疆四、小结:点的坐标与向量的坐标一般不同,只有表示向量的有向线段的起点是坐标原点时.有向线段终点的坐标与向量的坐标相同.这一点务必向学生讲清楚.;明确用向量坐标法证明或计算几何问题的基本步骤:建系设坐标→向量点的坐标化→向量的直角坐标运算奎屯王新敞新疆运用向量的坐标表示及其运算研究立体几何中的角、距离、证明垂直等问题时,关键是建立适当的坐标系,进而将向量坐标化,建立坐标系时,要充分利用图形的几何性质奎屯王新敞新疆掌握运用向量求角、距离的方法奎屯王新敞新疆五、课后作业:奎屯王新敞新疆4.(2009全国Ⅱ)如图,直三棱柱ABC-A1B1C1中,AB⊥AC,D、E分别为AA1、B1C的中点,DE⊥平面B1BCC1(Ⅰ)证明:AB=AC(Ⅱ)设二面角A-BD-C为60°,求B1C与平面BCD所成的角的大小【解析】(Ⅰ)以A为坐标原点,射线AB为x轴的正半轴,建立如图所示的直角坐标系A—xyz。设B(1,0,0),C(0,b,0),D(0,0,c),则1B(1,0,2c),E(12,2b,c).于是DE=(12,2b,0),BC=(-1,b,0).由DE⊥平面1BCC知DE⊥BC,DEBC=0,求得b=1,所以AB=AC。(Ⅱ)设平面BCD的法向量(,,),ANxyz则0,0.ANBCANBD又BC=(-1,1,0),BD=(-1,0,c),故00xyxcz令x=1,则y=1,z=1c,AN=(1,1,1c).又平面ABD的法向量AC�=(0,1,0)由二面角CBDA为60°知,,ACAN�=60°,故ACAN�=||||ACAN�60cosACANACAN°,求得21c于是AN�),,(211AN,1CB�),,211(1CB,1111cos,,2||||ANCBANCBANCB���1,ANCB�601CBAN,°所以CB1与平面BCD所成的角为30°5.(2009江西高考)如图,在四棱锥PABCD中,底面ABCD是矩形,PA平面ABCD,4PAAD,2AB.以BD的中点O为球心、BD为直径的球面交PD于点M.(1)求证:平面ABM⊥平面PCD;(2)求直线PC与平面ABM所成的角;(3)求点O到平面ABM的距离.OAPBCMD【解析】方法一:(1)依题设,M在以BD为直径的球面上,则BM⊥PD.因为PA⊥平面ABCD,则PA⊥AB,又AB⊥AD,所以AB⊥平面PAD,则AB⊥PD,因此有PD⊥平面ABM,所以平面ABM⊥平面PCD.ONAPBCMDzxy(2)设平面ABM与PC交于点N,因为AB∥CD,所以...