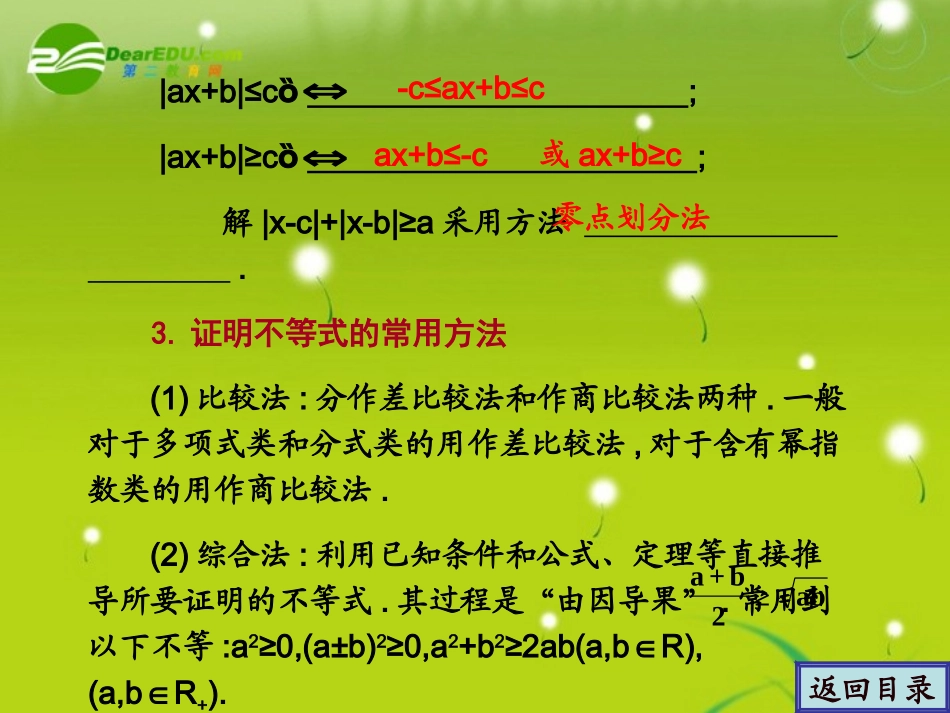
学案学案33不等式选讲不等式选讲返回目录1.绝对值不等式的性质在求最值时有其独特的作用,特别要注意等号成立的条件.|a+b|=|a|+|b|;|a-b|=|a|+|b|.⇔⇔ab≥0ab≤0返回目录|ax+b|≤c;|ax+b|≥c;解|x-c|+|x-b|≥a采用方法.3.证明不等式的常用方法(1)比较法:分作差比较法和作商比较法两种.一般对于多项式类和分式类的用作差比较法,对于含有幂指数类的用作商比较法.(2)综合法:利用已知条件和公式、定理等直接推导所要证明的不等式.其过程是“由因导果”.常用到以下不等:a2≥0,(a±b)2≥0,a2+b2≥2ab(a,bR),∈(a,bR∈+).⇔⇔零点划分法-c≤ax+b≤cax+b≤-c或ax+b≥cab≥2b+a(3)分析法:从求证的不等式出发,分析使这个不等式成立的条件,把证明不等式转化为判定这些条件是否具备的问题.这是一种“执果索因”的方法.(4)放缩法:依据不等式的传递性,具有一定的技巧性.常用的放缩法有:加项或减项、利用比例的性质、利用均值不等式、利用函数单调性,一定要把握好“度”,使其恰到好处.(5)换元法:注意新元的取值范围,保证等价性.(6)含有“至多”“至少”“唯一”“不大于”“不小于”等词语的,考虑用反证法.返回目录返回目录考点一考点一|ax+b|c)|ax+b|c)型不等式的解法型不等式的解法解不等式:(1)|2x-5|≤8;(2)|2-3x|>7.【【分析分析】】利用绝对值的意义,将绝对符号去掉.返回目录【【解析解析】】(1)由原不等式得-8≤2x-5≤8.∴-≤x≤.∴原不等式的解集为{x|-≤x≤}.(2)由原不等式得3x-2>7或3x-2<-7.∴x>3或x<-.故原不等式的解集为{x|x>3或x<-}.21323213233535返回目录【【评析评析】】含绝对值的不等式的解法,关键是利用绝对值的意义去掉绝对值.在变形过程中要特别注意保证同解,同时还要注意步骤的简捷与表达的明晰;区别“并”还是“交”的关键是“或”还是“且”,同时还要分清端点是否包括在内.*对应演练**对应演练*解不等式:3≤|x-2|<9.解法一解法一:原不等式等价于|x-2|≥3,|x-2|<9.x-2≥3或x-2≤-3,x≥5或x≤-1,-9c)|x-a|+|x-b|c)型不等式的解法型不等式的解法解不等式:|x-1|+|x+2|<5.【【分析分析】】这是一个含有两个绝对值符号的不等式,为了使其转化为不含绝对值符号的不等式,要对未知数x进行分类讨论,即用“零点划分法”将实数分成x<-2,-2≤x<1和x≥1三个部分进行讨论.【【解析解析】】解法一:用“零点划分法”将实数分类:令x-1=0得x=1;令x+2=0得x=-2.(1)当x<-2时,原不等式化为:-x+1-x-2<5,即x>-3.∴-3