高考数学一轮复习课件：7.2复数的四则运算1 课件VIP免费

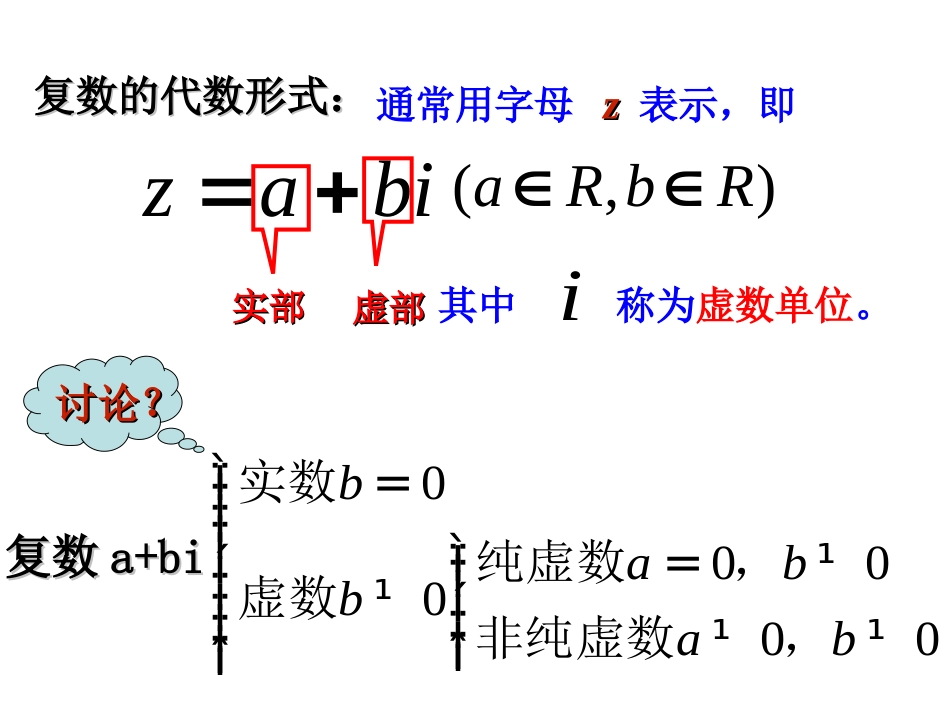
我们引入这样一个数我们引入这样一个数ii，把，把ii叫做叫做虚数单位，并且规定：虚数单位，并且规定：.复习：①i2=-1;②i可以与实数一起进行四则运算,并且加、乘法运算律不变.实部实部复数的代数形式：复数的代数形式：通常用字母zz表示，即biaz),(RbRa虚部虚部其中称为虚数单位。i讨论？讨论？复数复数a+bia+bi000000babbabì=ïïïïì=¹ïíïï¹íïïï¹¹ïîïî实数纯虚数，虚数非纯虚数，如果两个复数的如果两个复数的实部实部和和虚部虚部分别相分别相等，那么我们就说这等，那么我们就说这两个复数相等两个复数相等．,,,,Rdcba若dicbiadbca特别地，a+bi=0.a=b=03.2复数的四则运算1.复数加减法的运算法则：(1)运算法则:设复数z1=a+bi,z2=c+di,那么：z1+z2=(a+c)+(b+d)i;z1-z2=(a-c)+(b-d)i.即:两个复数相加(减)就是实部与实部,虚部与虚部分别相加(减).(2)复数的加法满足交换律、结合律,即对任何z1,z2,z3∈C,有z1+z2=z2+z1,(z1+z2)+z3=z1+(z2+z3).(3)复数的和与差仍然是一个复数例1.计算(56)(2)(34)iii-+---+解:(56)(2)(34)(523)(614)11iiiii-+---+=--+---=-2.复数的乘法(1)复数乘法的法则复数的乘法与多项式的乘法是类似的,但必须在所得的结果中把i2换成-1,并且把实部合并.即:(a+bi)(c+di)=ac+bci+adi+bdi2=(ac-bd)+(bc+ad)i.(2)复数乘法的运算定理复数的乘法满足交换律、结合律以及乘法对加法的分配律.即对任何z1,z2,z3有z1z2=z2z1;(z1z2)z3=z1(z2z3);z1(z2+z3)=z1z2+z1z3.1()()abiabi+-（）2()()abiabi++（）例2：计算222aabiabibi=-+-22ab=+222aabib=+-3(12)(34)(2)iii-+-+（）(12)(34)(2)(112)(2)2015iiiiii-+-+=--+=-+（1）已知求1232,14zizi=+=-121212,,,zzzzzz+-·巩固练习把满足(c+di)(x+yi)=a+bi(c+di≠0)的复数x+yi叫做复数a+bi除以复数c+di的商,()().abiabicdicdi++¸++记做或222222()()()()()()()abiabicdiabicdicdicdicdiacbdbcadiacbdbcadicdcdcd++-+¸+==++-++-+-==++++3.复数的除法例题3计算(1)(1+2i)÷(3-4i);(2)234ii--拓展求满足下列条件的复数z:(1)z(3－4i)=1;(2)(3+i)z=4+2i变式计算()()1412434iiii-++++思考：设Z=a+bi(a,bR∈)那么实部相等，虚部互为相反数的两个复数叫做互为共轭复数.复数z=a+bi的共轭复数记作?zz+=,zzabi=-?zz-=4.共轭复数：注：1）当a=0时，共轭复数也称为共轭虚数；2）实数的共轭复数是它本身。共轭复数的相关运算性质22ZZab·=+2Z2ZZaZbi+=-=5.复数的乘方：对任何及，有12,,zzzCÎ,mnN*Îmnmnzzz+×=()mnmnzz=1212()nnnzzzz×=×21i=-32iiii=×=-431iiiii=×=-×=1ii=特殊的有：一般地，如果，有Nn44142431,,1,nnnniiiiii+++===-=-2222()(),()2,(1(1)(2))2nzaainNaaiaaaia=+Î+=-=-若则有：：2322:(1)(2)(313,2213,21)210iiwwwww=-+=--=++=若则有：，。例求值：232006iiii++++234567820012002200320042005200612...01iiiiiiiiiiiiiiiii=++++++++++++++=++=-解：原式（）（）（）例设，求证：（1）；（2）i2321012.13证明：（1）22)2321()2321(11ii;04323412321ii22)23(23212)21(2321iii（2）33)2321(i)2321()2321(2ii)2321)(2321(ii22)23()21(i14341例题讲解例题讲解【练习】1、在复数范围内分解因式(1)x2+42、在复数范围内分解因式(1)x4-161112.22iii+++××220求()()...()例的值.20(120)21021052105426111122212()22iiiiiii+××××××´++++==éù+êú====êúëû1＋2＋3＋＋20原式()()=()()解：例题讲解例题讲解1.复数的四则运算；2.复数运算的乘方形式；3.共轭复数的相关运算性质；4.复数运算中的常用结论。课堂小结课堂小结2(tan)(2)0(),xxixiRaaa-+-+=Î设关于的方程若方程有实数根，求锐角的值并求出方程的所有根。拓展22(tan2)(1)0tan20,101,tan145oxxxixxxxaaaa--+--=\--=--=\=-=\=解：