浙江湖州市安吉县高一数学函数的单调性 课件VIP免费

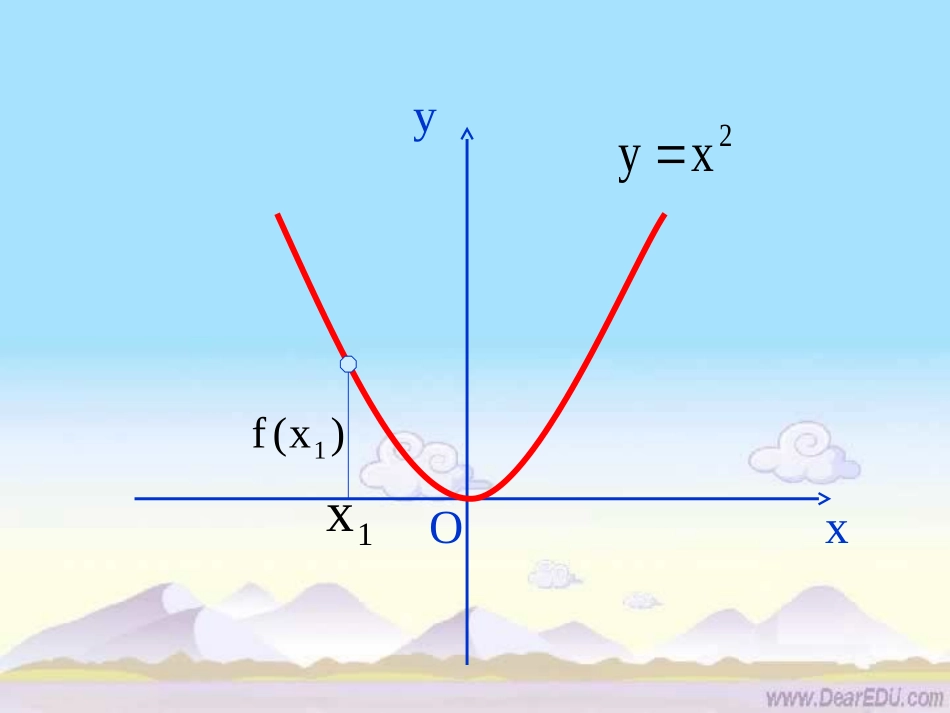
函数的单调函数的单调性性安吉昌硕高级中学安吉昌硕高级中学Oxy1x)x(f12xy课题引入Oxy1x)x(f12xyOxy1x)x(f12xyOxy1x)x(f12xyOxy1x)x(f12xyOxy1x)x(f12xyOxy1x)x(f12xyOxy1x)x(f12xyOx)x(f11xy2xy,,21xx在给定区间上任取21xx)f(x)f(x21函数f(x)在给定区间上为增函数。Oxy)x(fy如何用x与f(x)来描述上升的图象？)x(f11x如何用x与f(x)来描述下降的图象？,,21xx在给定区间上任取21xx函数f(x)在给定区间上为减函数。)f(x)f(x21)x(f1)x(f2)x(fyOxy1x2x)x(f22x如果对于属于定义域I内的某个区间上的任意两个自变量的值x1、x2，当x1＜x2时，都有f（x1）＜f（x2），那么就说f（x）在这个区间上是增函数.增函数与减函数定义说明：函数y=f(x)在区间D上是增函数或减函数，就称函数y=f(x)在区间D上具有单调性，D称为函数的单调区间。如果对于属于定义域I内的某个区间上的任意两个自变量的值x1、x2，当x1＜x2时，都有f（x1）>f（x2），那么就说f（x）在这个区间上是减函数.-5Oxy12345-1-2-3-4123-1-2例1.下图是定义在[－5，5]上的函数y＝f（x）的图象，根据图象说出y＝f（x）的单调区间，以及在每一单调区间上，y＝f（x）是增函数还是减函数.解：y＝f（x）的单调区间有[－5，－2），[－2，1），[1，3），[3，5].其中y＝f（x）在[－5，－2），[1，3）上是减函数，在[－2，1），[3，5）上是增函数.作图是发现函数单调性的方法之一.注意！用逗号间隔开单调递增区间：单调递减区间：]1,(),1[xx2x)x(f2y21o的单调区间判断函数练习xxxf2)(.12增函数减函数图象图象特征自左至右，图象上升.自左至右，图象下降.数量特征y随x的增大而增大.当x1＜x2时，y1＜y2y随x的增大而减小.当x1＜x2时，y1＞y2Oxyx1x2y1y2Oxyx2x1y1y2归纳：归纳：例2.证明函数f(x)=3x+2在R上是增函数。f(x1)-f(x2)=(3x1+2)-(3x2+2)由x1f(x2),则f(x)在这个区间上是减函数上呢？在（减函数？证明你的结论上是增函数还是在函数例)0,.),0(1)(.3xxf证明：证明：设x1，x2∈（0，+∞），且x1＜x222111)(,1)(xxfxxf则212111)()(xxxfxf2112xxxx0),0(,2121xxxx01221xxxx0)()(21xfxf)()(21xfxf.),0(1)(上是减函数在函数xxf1－1－1Oxy1（作差）（取值）（变形）（定号）（判断）1－1－1Oxy1问题：f（x）在定义域上是减函数吗？取x1=-1，x2=1，f（-1）=-1f（1）=1，-1＜1f（-1）＜f（1）可见x1f(x2)不一定成立。f（x）在定义域上不是减函数，其单调递减区间为（－∞，0），（0，＋∞）x1题型二：图象法对单调性的判断例4：指出下列函数的单调区间：12xy如果函数的图象比较好画，我们就画图象观察——图象法利用图象法求单调区间的时候，应特别注意某些特殊点，尤其是图象发生急转弯的地方。用它们将定义域进行划分，再分别考察。练习2：已知32)(2xxxf作出f(x)的图象，并指出其单调区间。)0(32)0(3222xxxxxxy上单调递减；、在区间]1,0(]1,()(xf.),1(]0,1(上单调递增、在区间31-1-3-3Oxy函数解析式为解：课堂小结课堂小结2.2.单调性的证明步骤：单调性的证明步骤：1.1.函数单调性定义：函数单调性定义：如果对于属于如果对于属于定义域定义域II内某个区间上内某个区间上的的任意两任意两个自变量个自变量xx11、、xx22的值，当的值，当xx11