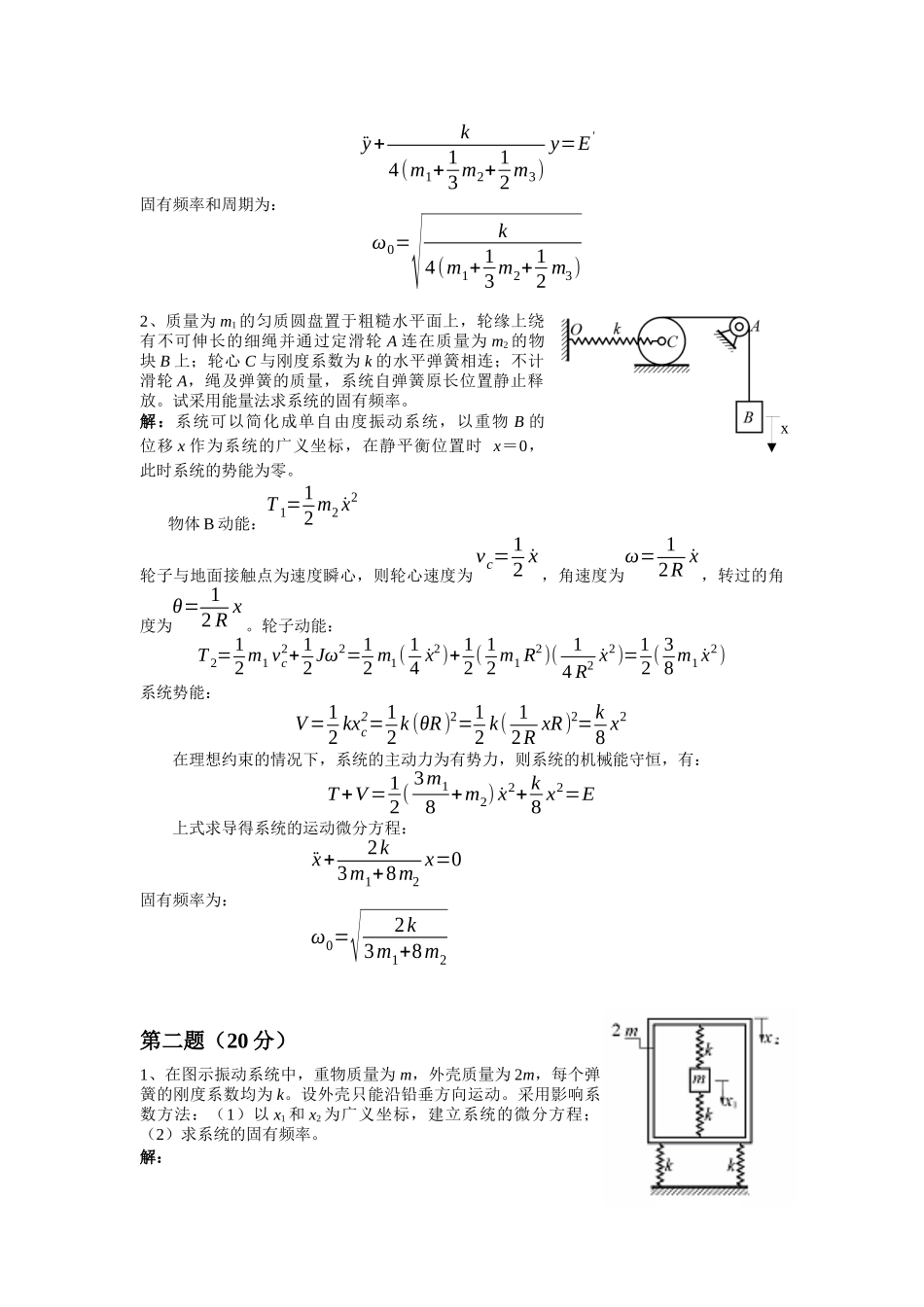
2008 年振动力学期末考试试题第一题(20 分)1、在图示振动系统中,已知:重物 C 的质量 m1,匀质杆 AB 的质量 m2,长为 L,匀质轮 O 的质量 m3,弹簧的刚度系数 k。当 AB 杆处于水平时为系统的静平衡位置。试采用能量法求系统微振时的固有频率。解:系统可以简化成单自由度振动系统,以重物 C 的位移 y 作为系统的广义坐标,在静平衡位置时 y=0,此时系统的势能为零。AB 转角:ϕ= y/L系统动能:m1动能:T 1=12 m1 ˙y2m2动能:T 2=12 J2 ω22=12 ( 13 m2 L2) ˙ϕ2=12( 13 m2 L2)( ˙yL )2=12 ( 13 m2) ˙y2m3动能:T 3=12 J 3ω32=12( 12 m3 R2)( ˙yR )2=12 ( 12 m3) ˙y2系统势能:V=−m1gy+m2 g( 12 y )+ 12 k( 12 y)2在理想约束的情况下,系统的主动力为有势力,则系统的机械能守恒,因而有:T+V=12( m1+ 13 m2+12 m3) ˙y2−m1 gy+ 12 m2 gy+ 12 k( 12 y )2=E上式求导,得系统的微分方程为:x¨y+k4(m1+ 13 m2+ 12 m3)y=E'固有频率和周期为:ω0=√k4(m1+ 13 m2+ 12 m3)2、质量为 m1 的匀质圆盘置于粗糙水平面上,轮缘上绕有不可伸长的细绳并通过定滑轮 A 连在质量为 m2 的物块 B 上;轮心 C 与刚度系数为 k 的水平弹簧相连;不计滑轮 A,绳及弹簧的质量,系统自弹簧原长位置静止释放。试采用能量法求系统的固有频率。解:系统可以简化成单自由度振动系统,以重物 B 的位移 x 作为系统的广义坐标,在静平衡位置时 x=0,此时系统的势能为零。物体 B 动能:T 1=12 m2 ˙x2轮子与地面接触点为速度瞬心,则轮心速度为vc=12 ˙x,角速度为ω= 12R ˙x,转过的角度为θ= 12 R x。轮子动能:T 2=12 m1 vc2+ 12 Jω2=12 m1( 14 ˙x2)+ 12( 12 m1 R2)( 14 R2 ˙x2)=12( 38 m1 ˙x2)系统势能:V=12 kxc2=12 k (θR)2=12 k( 12R xR)2=k8 x2在理想约束的情况下,系统的主动力为有势力,则系统的机械能守恒,有:T+V=12( 3m18 +m2) ˙x2+ k8 x2=E上式求导得系统的运动微分方程:¨x+2k3m1+8m2x=0固有频率为:ω0=√2k3m1+8m2第二题(20 分)1、在图示振动系统中,重物质量为 m,外壳质量为 2m,每个弹簧的刚度系数均为 k。设外壳只能沿铅垂方向运动。采用影响系数方法:(1)以 x1 和 x2 为广义坐标,建立系统的微分方程;(2)求系统的固有频率。解:x1x2DkL32kL311k11k系统为二自由度...