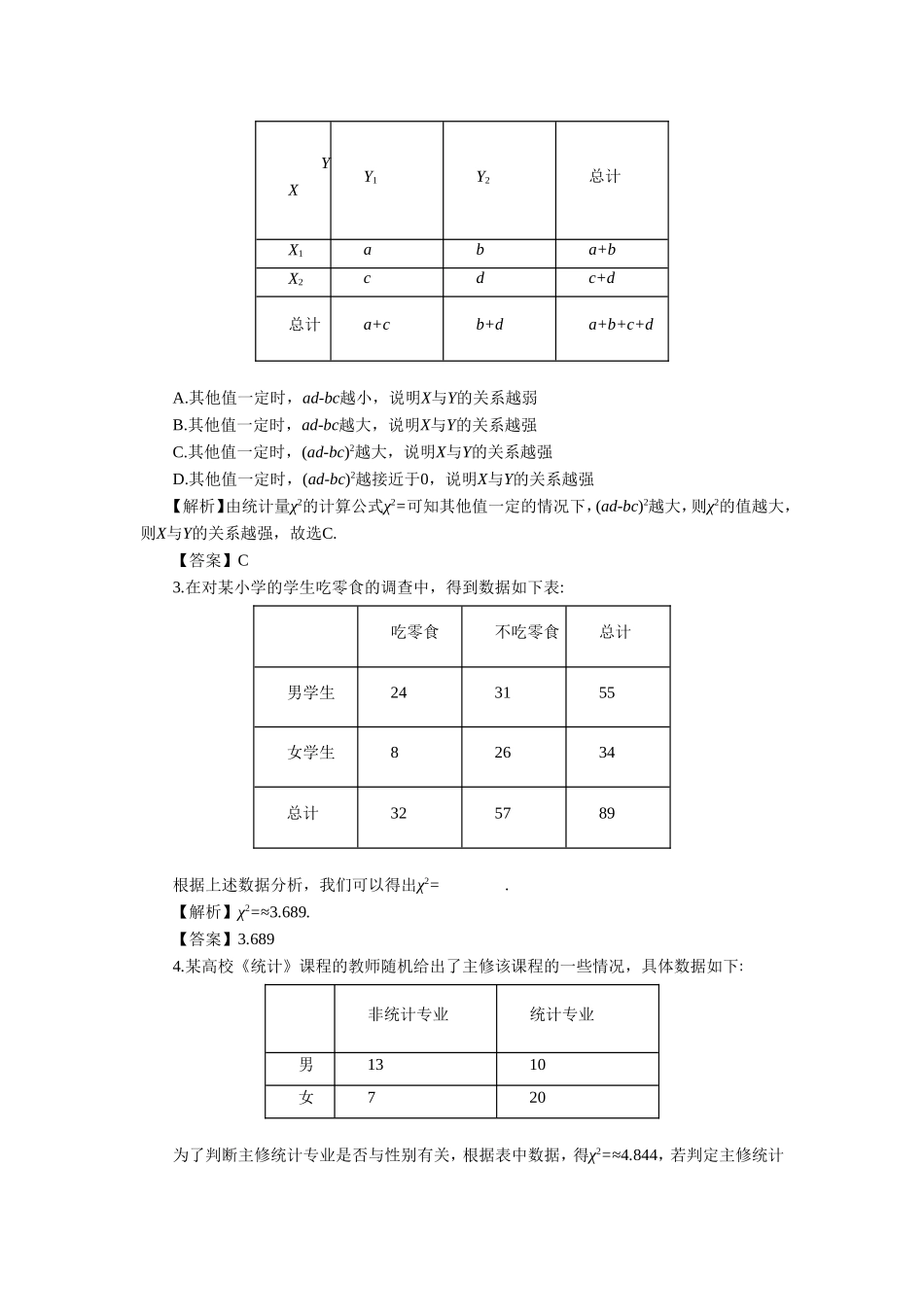
《3.2.1 独立性检验》 导学案学习目标1.通过对典型案例(如“患肺癌与吸烟有关吗”等)的探究.了解独立性检验(只要求2×2列联表)的基本思想、方法及初步应用.2.过程与方法:引导学生形成 “自主学习”“合作学习”等良好的学习方式,培养学生的归纳概括能力.重点了解独立性检验的基本思想.难点独立性检验的基本思想、随机变量χ2的含义及独立性检验的步骤.教学过程经常上网会影响学习吗?下表为教育部对1000名中学生进行调查的结果.经常上网影响学习吗?如何判断?经常上网不经常上网合计不及格80120200及格120680800合计2008001000问题1:(1)通过上述数据经常上网的人成绩及格的比例为 60% ,不经常上网的人成绩及格的比例为 85% ,这个数据可以初步判断经常上网对学习成绩是有影响的,但这种说法的把握性有多大,还需要进行独立性检验才知道. (2)独立性检验的概念用统计量χ2的大小来研究两个变量是否有关系的方法,称为独立性检验.问题2:两个分类变量A和B的2×2列联表一般地,假设有两个分类变量A和B,它们的可能取值分别为{A1,A2}和{B1,B2}, 其样本频数列联表(称为2×2列联表)为: BA B1B2总计A1ab a+b A2cd c+d 总计 a+c b+d a+b+c+d 问题3:统计量χ2的计算公式是怎样的?若有如下列联表所示的抽样数据:类1类2总计类 Aaba+b类 Bcdc+d总计a+cb+da+b+c+d 则χ2= (其中n=a+b+c+d). 问题4:根据χ2判断两变量是否有关联当χ2≤2.706时, 没有 充分的证据判定变量A、B有关联,可以认为变量A、B是 没有 关联的; 当χ2>2.706时,有 90% 的把握判定变量A、B有关联; 当χ2>3.841时,有 95% 的把握判定变量A、B有关联; 当χ2>6.635时,有 99% 的把握判定变量A、B有关联. 独立性检验的必要性为什么不能只凭列联表中的数据和由其绘出的图形下结论?由列联表可以粗略地估计出两个分类变量是否有关(即粗略地进行独立性检验),但2×2列联表中的数据是样本数据,它只是总体的代表,具有随机性,故需要用独立性检验的方法确认所得结论在多大程度上适用于总体.学习交流1.在吸烟与患肺病是否相关的研究中,有下面的说法:①若χ2=6.7,我们有99%的把握判定吸烟与患肺病有关联,那么在100个吸烟的人中必有99个患肺病;②从独立性检验可知有99%的把握判定吸烟与患肺病有关联时,若某人吸烟,那么他有99%的可能患有肺病;③从统计量中求出有95%的把握判定吸烟与患肺病有关联,是指有5%的可能性使得推断出现错误.其中说法正确的...