高三数学函数的极限一 新课标 人教版 课件VIP免费

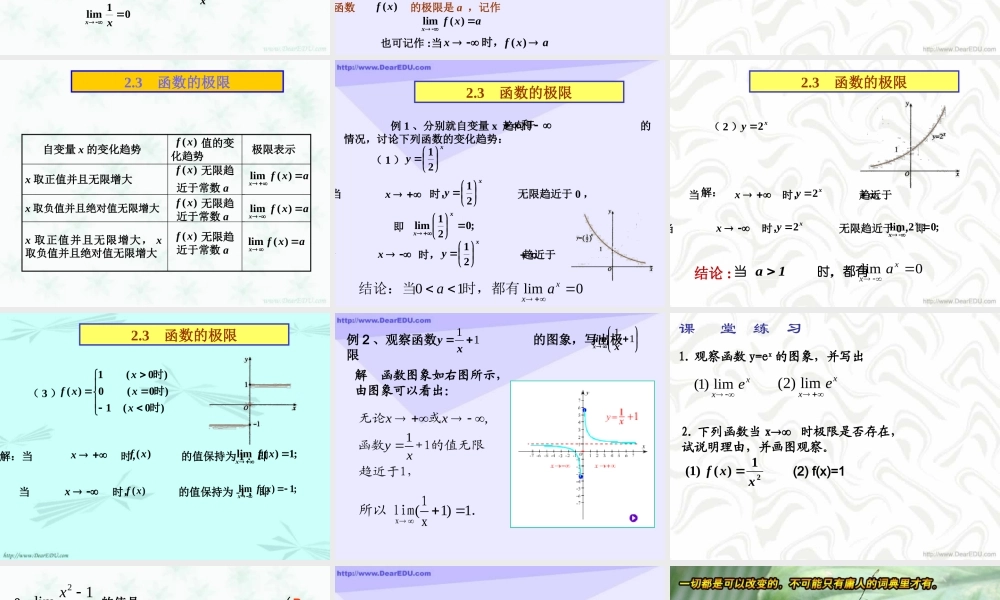
复习1 、数列的极限：如果当项数 n 无限增大，数列的项 an 无限趋近于某个常数 a （即 | an - a | 无限地接近于 0 ），称数列 {an} 以 a 为极限。aannlim数列 {an} 以 a 为极限，记作2 、常见数列的极限 如：③ 当 |a|<1 时，则0limnna01lim nn①)(lim为常数CCCn②3 、数列与函数的关系：数列可以看作是定义在正整数集上的一种特殊函数。 1观察函数y的图象,当x时的变化趋势。x无论 x+ 或 x- 的值无限趋近于0.x1函数y 0.x1时，当x即2.3 函数的极限x110100100010000100000···y10.10.010.0010.00010.00001···考察函数 当 x 无限增大时的变化趋势．xy1yxO 当自变量 x 取正值并无限增大时，函数 的值无限趋近于 0 ，即 |y-0| 可以变得任意小．xy1当 x 趋向于正无穷大时，函数xy1的极限是 0 ，记作01limxx2.3 函数的极限yxOxy1当 x 趋向于负无穷大时，函数的极限是 0 ，记作01limxx2.3 函数的极限就说当 x 趋向于正无穷大时，函数 的极限是 a ，记作axfx)(lim)(xf一般地，当自变量 x 取正值并且无限增大时，如果函数)(xf无限趋近于一个常数 a ，也可记作 : 当axfx)(时，当就说当 x 趋向于负无穷大时，函数 的极限是 a ，记作axfx)(lim当自变量 x 取负值并且绝对值无限增大时，如果函数)(xf无限趋近于一个常数 a ，也可记作 :axfx)(时，)(xf2.3 函数的极限如果axfaxfxx)(lim)(lim且那就是说当 x 趋向于axfx)(lim也可记作 :当axfx)(时，无穷大时，函数 的极限是 a ，记作)(xfCxfx)(lim对于常数函数)()(RxCxf也有2.3 函数的极限x 取正值并且无限增大axfx)(lim 无限趋近于常数 a )(xf极限表示 值的变化趋势 自变量 x 的变化趋势 )(xfx 取负值并且绝对值无限增大axfx)(lim 无限趋近于常数 a )(xfx 取正值并且无限增大， x取负值并且绝对值无限增大axfx)(lim 无限趋近于常数 a )(xf2.3 函数的极限 例 1 、分别就自变量 x 趋向于 的情况，讨论下列函数的变化趋势：和（ 1 ）xy 21解：当 时， 无限趋近于 0 ，xy 21;021limxx即x当 时， 趋近于.xy 21x0lim10...