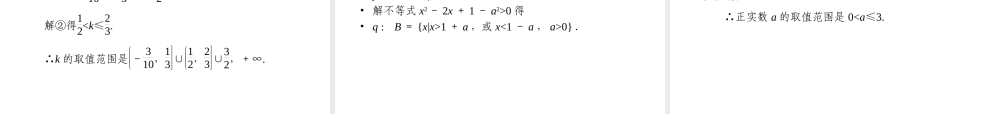章末归纳总结• 1 .学习命题,首先根据能否判断语句的真假看是否是命题,掌握四种命题的组成及互为逆否命题的等价性.• 2 .由于原命题和它的逆否命题是等价的,所以当一个命题的真假不易判断时,往往可以转而判断它的逆否命题的真假;有的命题不易直接证明时,就可以改证它的逆否命题成立,所以反证法的实质就是证明“原命题的逆否命题成立”,所以教材在阐述了四种命题后安排了用反证法的例题,可以加深对命题等价性理解.• 3 .要注意:否命题与命题的否定是不同的,如果原命题是“若 p 则 q” ,那么这个原命题的否命题是“若非 p ,则非 q” ,而这个命题的否定是“若 p 则非 q” ,可见:否命题既否定条件又否定结论,而命题的否定只否定结论,例如,原命题“若∠ A =∠ B ,则 a = b” 的否命题是“若∠ A≠∠B ,则 a≠b” ,而原命题的否定是“若∠ A =∠ B ,则 a≠b.”• 4 .充要条件的判断是通过判断命题“若 p 则 q” 的真假来判断的.因此,充要条件与命题的四种形式之间的关系密切,可相互转化.• 充分、必要条件问题涉及的知识面广,要深刻理解充分、必要条件的概念,而且要熟知问题中所涉及到的知识点和有关概念.• 5 .准确理解逻辑联结词“或”、“且”、“非”的含义,熟练判断“ p∧q” 、“ p∨q” 、“ ¬p” 形式的命题的真假.• 6 .准确区分全称命题和特称命题的差异,能用简洁、自然的语言表述含有一个量词的命题的否定.• [ 例 1] 判断下列命题的真假.• (1)∀x∈R ,若 x - 3 = 0 ,则 x - 3≤0 ;• (2) 若 x = 3 或 x = 5 ,则 (x - 3)(x - 6) = 0.• [ 解析 ] (1) x - 3 = 0⇒x - 3≤0 ,∴命题为真.• (2) 当 x = 5 时, (x - 3)(x - 6)≠0 ,∴命题为假.• [ 点评 ] (1) 实际上是“ p∨q” 命题的真假.• (2) 中实质上是 x∈{3,5} 时,有 (x - 3)(x - 6) = 0 ,显然是错误的,它不是“ p∨q” 形式的复合命题.• 分别指出由下列各组命题构成的“ p∨q” 、“ p∧q” 、“ ¬p”形式的复合命题的真假.• (1)p :正多边形有一个内切圆; q :正多边形有一个外接圆.• (2)p :角平分线上的点到角两边距离不相等; q :线段中垂线上的点到线段的两端点距离相等.• (3)p : 2∈{2,3,4} ; q : { 矩形 }∩{ 菱形...