山西省忻州市高考数学 专题 等比数列1复习课件VIP免费

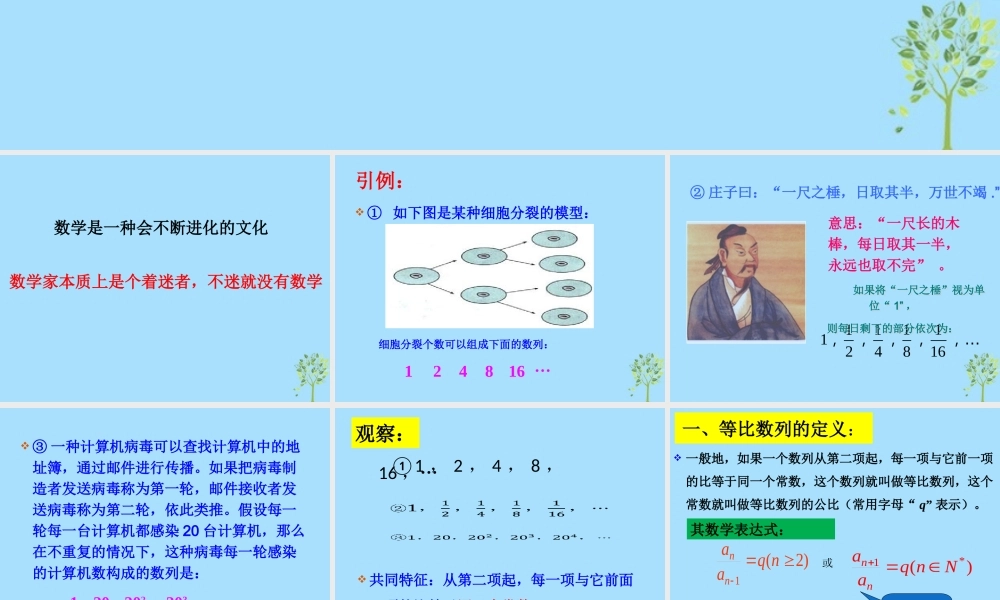
等比数列数学是一种会不断进化的文化数学家本质上是个着迷者，不迷就没有数学引例： ① 如下图是某种细胞分裂的模型：细胞分裂个数可以组成下面的数列：124816 …② 庄子曰：“一尺之棰，日取其半，万世不竭 .”意思：“一尺长的木棒，每日取其一半，永远也取不完” 。11111 24816，，，，，… 如果将“一尺之棰”视为单位“ 1” ，则每日剩下的部分依次为： 如果将“一尺之棰”视为单位“ 1” ，则每日剩下的部分依次为： ③ 一种计算机病毒可以查找计算机中的地址簿，通过邮件进行传播。如果把病毒制造者发送病毒称为第一轮，邮件接收者发送病毒称为第二轮，依此类推。假设每一轮每一台计算机都感染 20 台计算机，那么在不重复的情况下，这种病毒每一轮感染的计算机数构成的数列是：120202203…观察： 共同特征：从第二项起，每一项与它前面一项的比等于同一个常数；①1 ， 2 ， 4 ， 8 ，16 ，…一、等比数列的定义：  一般地，如果一个数列从第二项起，每一项与它前一项的比等于同一个常数，这个数列就叫做等比数列，这个常数就叫做等比数列的公比（常用字母“ q” 表示）。)2(1nqaann或)(*1Nnqaann其数学表达式：0na判别下列数列是否为等比数列 ? (2)1.2, 2.4 , -4.8 , -9.6 ……(3)2, 2, 2, 2, … (4)1, 0, 1, 0 ……(5) a, a, a, a, a …练一练练一练是不是是不是q =22,21,22,1,2)1(q = 1……不一定0a二、等比数列的通项公式：  法一：不完全归纳法等差数列daa12daa213daa314……由此归纳等差数列的通项公式可得： dnaan)1(1 法二：叠加法daa12daa23daa34……dnaan)1(1daann 1+ ）等差数列(2)1 ， 3 ， 9 ， 27 ， 81 ， 243 ，…(3) 5 ， 5 ， 5 ， 5 ， 5 ，5 ，…(4) 1 ， -1 ， 1 ， -1 ， 1 ，…(1)2 ， 4 ， 8 ， 16 ， 32 ， 64.12 22nnna 111 33nnna 15 15nna 1( 1)nna 思考：下面数列是等比数列吗？公比是什么？ 通项公式分别是什么？1111nnmmaa qaa q解：由等比数列的通项公式可知 n mnmaa q 探究已知等比数列的公比为 q, 第 m 项为 ，求 .已知等比数列的公比为 q, 第 m 项为 ，求 .mana不比智力，比努力；不比起步，比进步。可以失败，不可以失志；可以失望，不可以绝望。当今之世，舍我其谁！