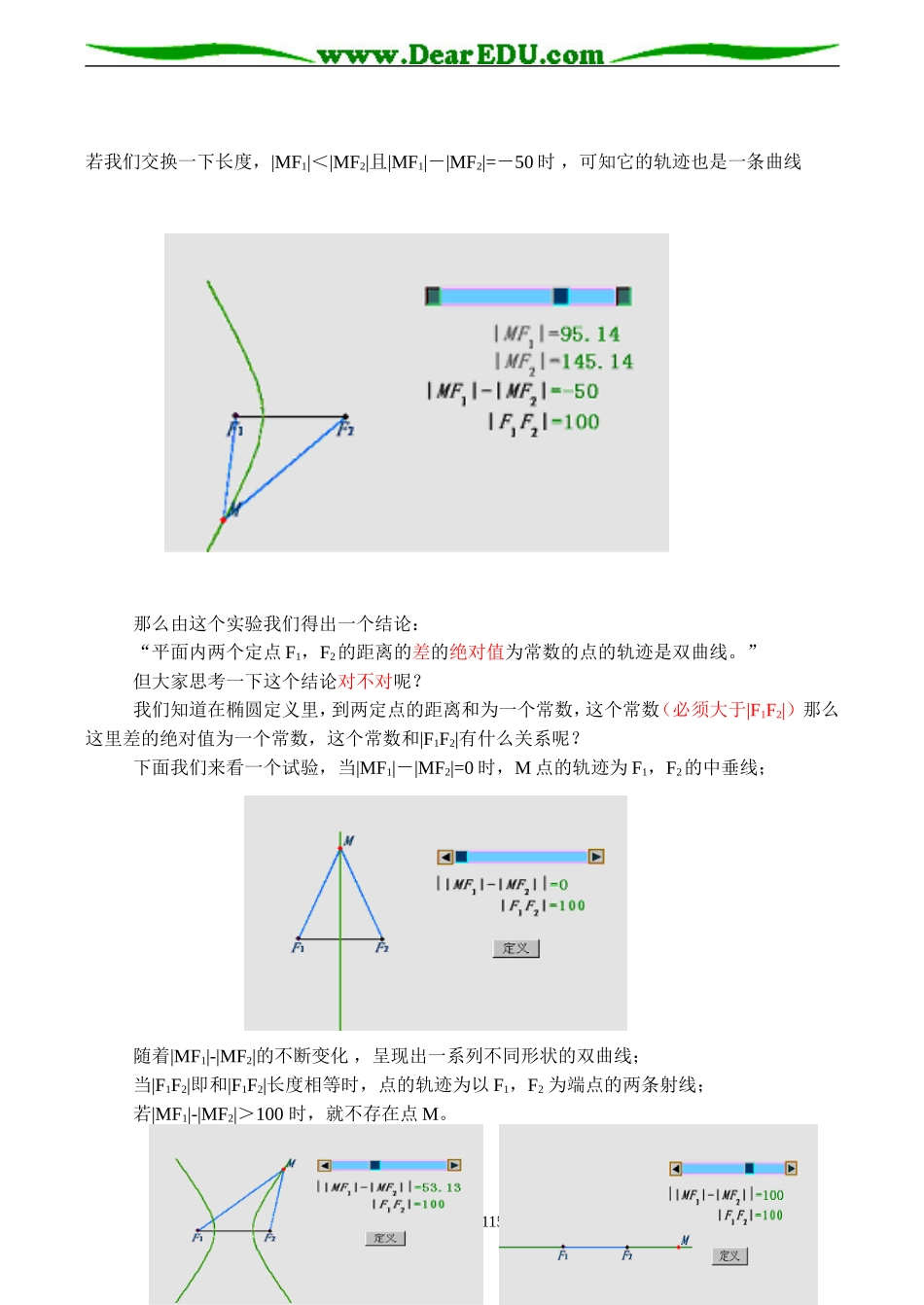
高二数学 双曲线及其标准方程(第一课时)一、教学目标㈠知识点① 双曲线及其焦点,焦距的定义。② 双曲线的标准方程及其求法。③ 双曲线中 a,b,c 的关系。④ 双曲线与椭圆定义及标准方程的异同。㈡能力要求① 使学生掌握双曲线的定义和标准方程的推导方法。② 由双曲线的标准方程知它的图形特征及焦点位置。③ 掌握 a,b,c 之间的关系。二、教学重点① 双曲线的定义。② 双曲线的标准方程。③ 掌握 a,b,c 之间的关系。三、教学难点 双曲线的标准方程。四、教学方法类比归纳法。(通过前面所学的椭圆进行联想,类比推出双曲线的定义及其标准方程,从而进行归纳总结)五、教学过程前面我们学习过椭圆,知道“平面内与两定点 F1,F2的距离的和等于常数(大于 F1F2 )的点的轨迹叫做椭圆”。下面我们来考虑这样一个问题?平面内与两定点 F1,F2的距离差为常数的点的轨迹是什么?我们在平面上固定两个点 F1,F2,平面上任意一点为 M,假设|F1F2|=100,|MF1|>|MF2|且|MF1|-|MF2|=50 不断变化|MF1|和|MF2|的长度,我们可以得出它的轨迹为一条曲线。用心 爱心 专心 115 号编辑若我们交换一下长度,|MF1|<|MF2|且|MF1|-|MF2|=-50 时 ,可知它的轨迹也是一条曲线那么由这个实验我们得出一个结论:“平面内两个定点 F1,F2的距离的差的绝对值为常数的点的轨迹是双曲线。”但大家思考一下这个结论对不对呢?我们知道在椭圆定义里,到两定点的距离和为一个常数,这个常数(必须大于|F1F2|) 那么这里差的绝对值为一个常数,这个常数和|F1F2|有什么关系呢?下面我们来看一个试验,当|MF1|-|MF2|=0 时,M 点的轨迹为 F1,F2的中垂线;随着|MF1|-|MF2|的不断变化 ,呈现出一系列不同形状的双曲线;当|F1F2|即和|F1F2|长度相等时,点的轨迹为以 F1,F2 为端点的两条射线;若|MF1|-|MF2|>100 时,就不存在点 M。用心 爱心 专心 115 号编辑那么由以上的一些试验我们可以得出双曲线的准确定义:定义:平面内与两定点 F1,F2的距离差的绝对值为非零常数(小于|F1F2|)的点的轨迹是双曲线。定点 F1,F2叫做双曲线的焦点,两焦点的距离叫双曲线的焦距。我们知道当一个椭圆中心在原点,焦点在坐标轴上时,所表示椭圆的方程为标准方程。当 焦 点 在 x 轴 上 时 ,; 当 焦 点 在 y 轴 上 时 ,那么双曲线方程是否也有标准方程呢?我们就来求一下看看:解:建立直角坐标系 xoy,使 x 轴经过 ...