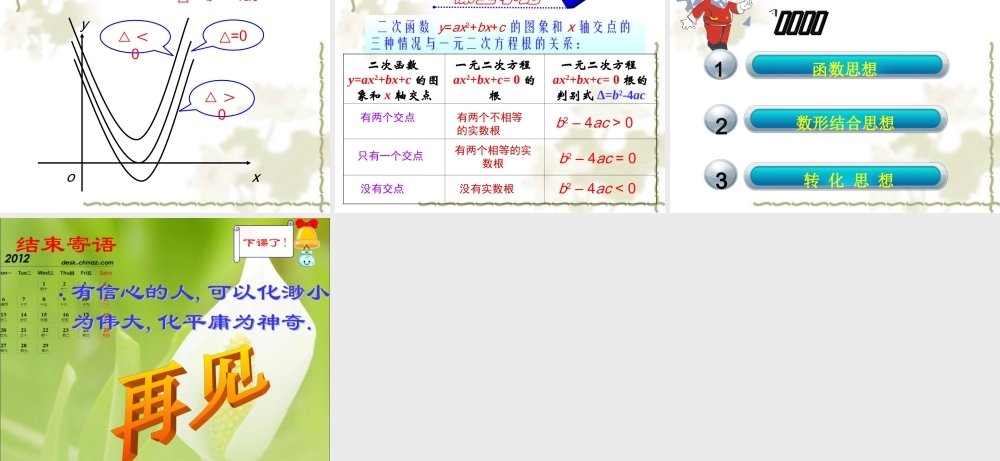
义务教育课程标准实验教科书九年级 下册26.2 用函数观点看一元二次方程 当 y = 0 时,回顾旧知2yaxbxc二次函数的一般式:( a≠0 )______ 是自变量, ____ 是 ____ 的函数。xyxax² + bx + c =0ax² + bx + c = 0这是什么方程? 九年级上册中我们学习了“一元二次方程” 一元二次方程与二次函数有什么关系?学习目标【学 习 目 标】 1 .知道二次函数与一元二次方程的关系. 2 .会用一元二次方程 ax2 + bx + c = 0 根的判别式△= b2 - 4ac 判断二次函数 y = ax2+ bx + c 与 x 轴的交点的个数. 【学习重难点】 函数←→方程←→ X 轴交点,三者之间的关系的理解与运用。【学习重难点】 函数←→方程←→ X 轴交点,三者之间的关系的理解与运用。 • 2 、解方程:( 1 ) x2+ x - 6 = 0 ( 2 ) x2+4x+4 = 0 ( 3 ) 2x2-3x+5=0 问题 1: 如图 , 以 40 m /s 的速度将小球沿与地面成 30度角的方向击出时 , 球的飞行路线是一条抛物线 , 如果不考虑空气阻力 , 球的飞行高度 h ( 单位 :m) 与飞行时间 t ( 单位 :s) 之间具有关系 :h= 20 t – 5 t2 考虑下列问题 :(1) 球的飞行高度能否达到 15 m ? 如能 , 需要多少时间 ?(2) 球的飞行高度能否达到 20 m ? 如能 , 需要多少时间 ?(3) 球的飞行高度能否达到 20.5 m ? 为什么 ?(4) 球从 飞出到落地 要用多少时间 ?15= 20 t – 5 t2h=0h t20= 20 t – 5 t220.5= 20 t – 5 t20= 20 t – 5 t2解:( 1 )当 h = 15 时,20 t – 5 t 2 = 15t 2 - 4 t + 3 = 0t 1 = 1 , t 2 = 3当球飞行 1s 和 3s 时,它的高度为 15m .1s3s15 mh t2s ( 2 )当 h = 20 时,20 t – 5 t 2 = 20t 2 - 4 t + 4 = 0t 1 = t 2 = 2当球飞行 2s 时,它的高度为 20m .2s20 mh t ( 3 )当 h = 20.5 时,20 t – 5 t 2 = 20.5t 2 - 4 t + 4.1 = 0因为 ( - 4)2 - 4×4.1 < 0 ,所以方程无实根。球的飞行高度达不到 20.5 m.20.5 mh t ( 4 )当 h = 0 时,20 t – 5 t 2 = 0t 2 - 4 t = 0t 1 = 0 , t 2 = 4当球飞行 0s 和 4s 时,它的高度为 0m ,即 0s 时,球从地面飞出, 4s 时...