简谐运动的能量VIP免费

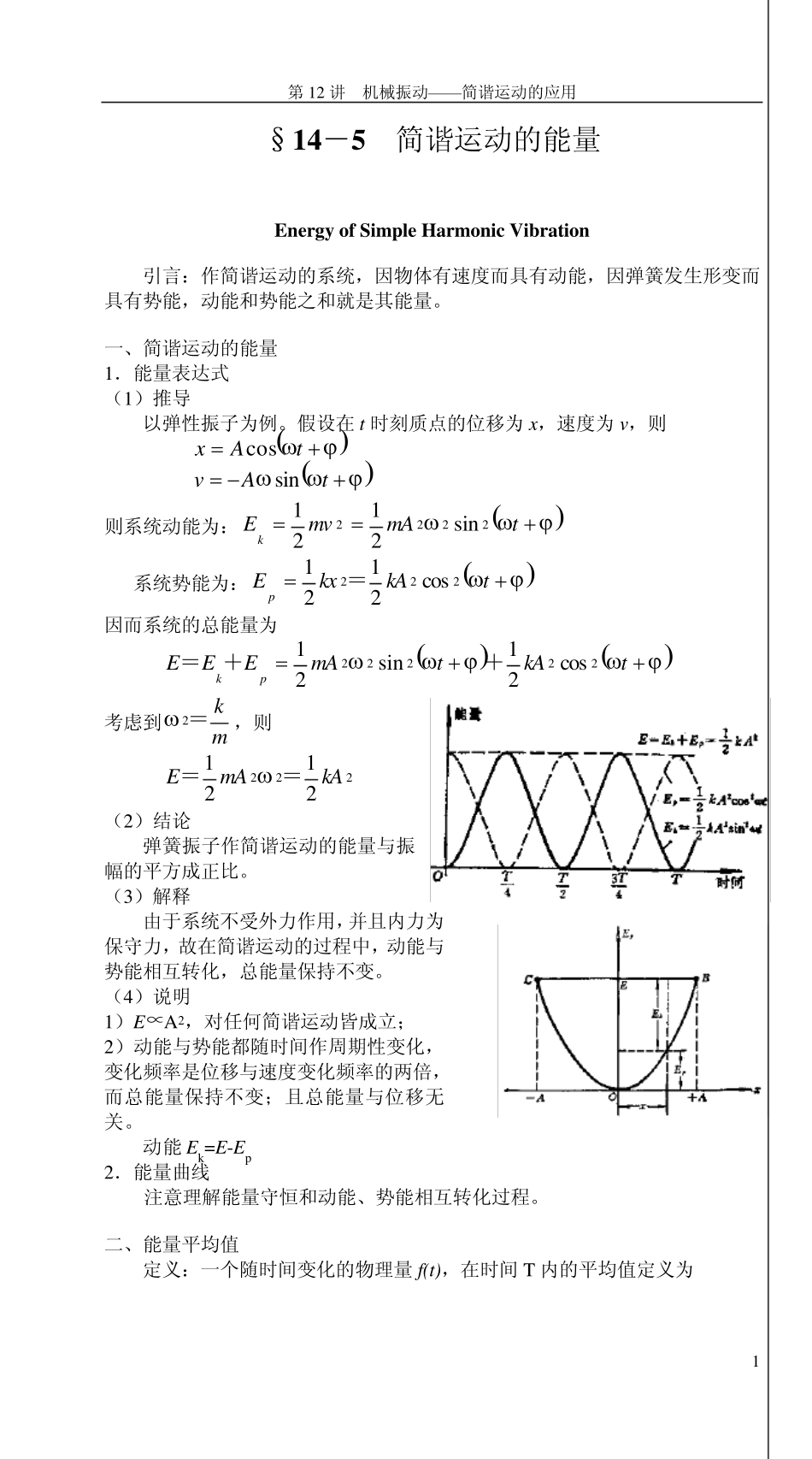
第12 讲 机械振动——简谐运动的应用 1 §14－5 简谐运动的能量 Energy of Simple Harmonic Vibration 引言：作简谐运动的系统，因物体有速度而具有动能，因弹簧发生形变而具有势能，动能和势能之和就是其能量。 一、简谐运动的能量 1．能量表达式 （1）推导 以弹性振子为例。假设在 t 时刻质点的位移为 x ，速度为 v ，则  tAxcos tAvsin 则系统动能为：tmAmvEk2222sin2121 系统势能为： tkAkxEp222cos2121＝ 因而系统的总能量为 tkAtmAEEEpk22222cos21sin21＋＋＝ 考虑到mk＝2，则 2222121kAmAE＝＝ （2）结论 弹簧振子作简谐运动的能量与振幅的平方成正比。 （3）解释 由于系统不受外力作用，并且内力为保守力，故在简谐运动的过程中，动能与势能相互转化，总能量保持不变。 （4）说明 1）E∝A2，对任何简谐运动皆成立； 2）动能与势能都随时间作周期性变化，变化频率是位移与速度变化频率的两倍，而总能量保持不变；且总能量与位移无关。 动能 Ek=E-Ep 2．能量曲线 注意理解能量守恒和动能、势能相互转化过程。 二、能量平均值 定义：一个随时间变化的物理量 f(t)，在时间 T 内的平均值定义为 第12 讲 机械振动——简谐运动的应用 2  TttfTf0d1 因而弹簧振子在一个周期内的平均动能为 22202224141dsi n211kAmAttmATETk  因而弹簧振子在一个周期内的平均势能为 TpmAkAttkATE0222224141dcos211＝ 结论：简谐运动的动能与势能在一个周期内的平均值相等，它们都等于总能量的一半。 三、应用 1．应用1——记忆振幅公式 由能量守恒关系可得：k A2/2= mv 02/2+ kx 02/2 解之即得： 2020 vxA＝ 2．应用2——推导简谐运动相关方程 在忽略阻力的条件下，作简谐运动的系统只有动能和势能（弹性势能和重力势能），且二者之和保持不变，因而有  0ddpkEEt 将具体问题中的动能与势能表达式代入上式，经过简化后，即可得到简谐运动的微分方程及振动周期和频率。这种方法在工程实际中有着广泛的应用。 此方法对于研究非机械振动非常方便。 例 1．用机械能守恒定律求弹簧振子的运动方程。 解：弹簧振子在振动过程中，机械能守恒，即 CkAkxmv222212121 两边对时间求导，得 0dd221dd221txxktvv...