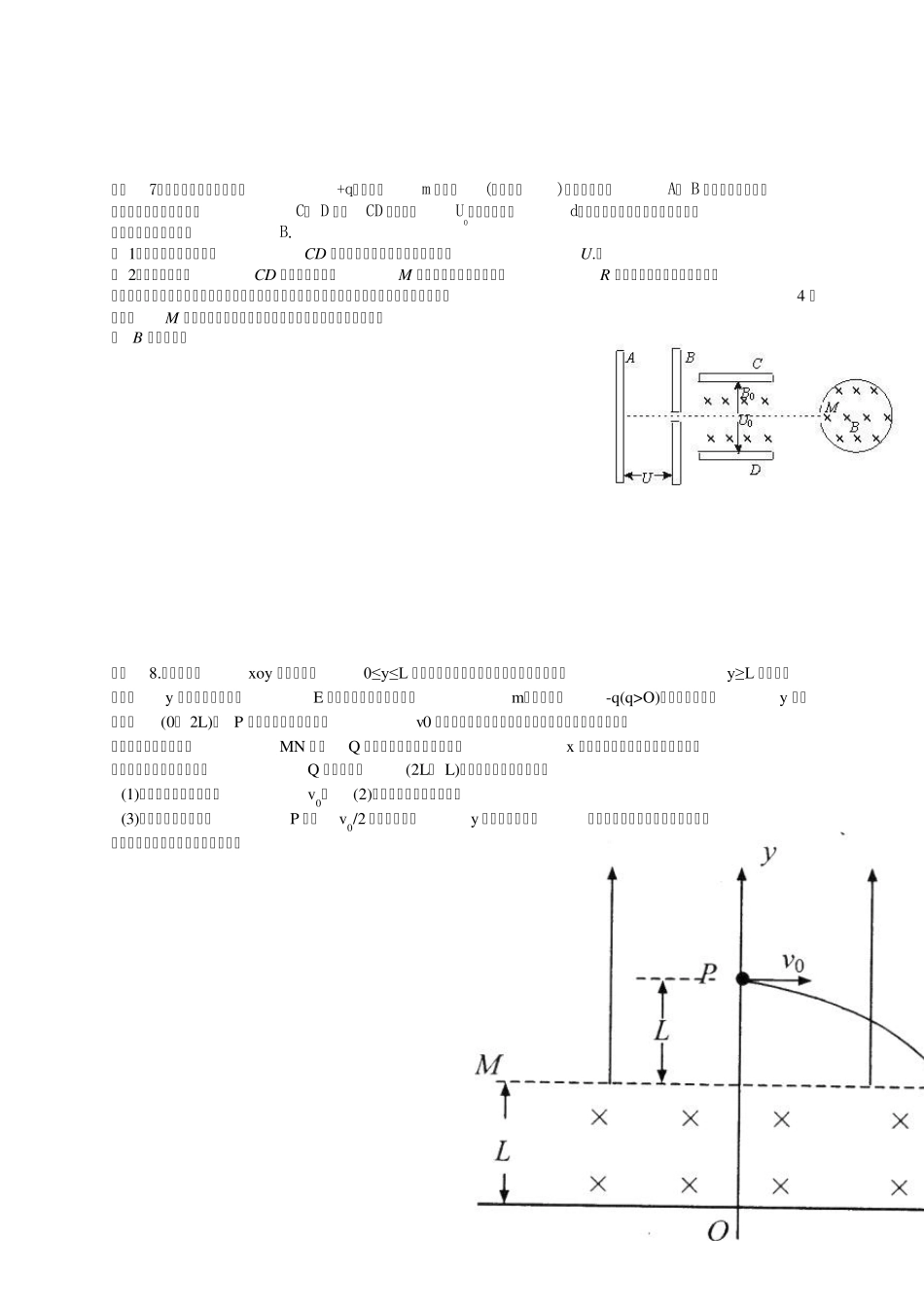
2012 高考物理专题:带电粒子在场中的运动(磁场边界问题) 专题一:带电粒子在场中的运动 练习1、如图所示的坐标系,x 轴沿水平方向,y 轴沿竖直方向。在x 轴上方空间的第一、第二象限内,既无电场也无磁场,在第三象限,存在沿y 轴正方向的匀强电场和垂直xy 平面(纸面)向里的匀强磁场,在第四象限,存在沿y 轴负方向、场强大小与第三象限电场场强相等的匀强电场。一质量为 m、电荷量为q 的带电质点,从y 轴上y=h 处的P1 点以一定的水平初速度沿x 轴负方向进入第二象限。然后经过x 轴上x=- 2h 处的P2 点进入第三象限,带电质点恰好能做匀速圆周运动。之后经过y轴上y=- 2h 处的P3 点进入第四象限。已知重力加速度为g。试求:1)粒子到达P2 点时速度的大小和方向2)第三象限空间中电场强度和磁感应强度的大小3)带电质点在第四象限空间运动过程中最小速度的大小和方向。 练习2 . 如图,在 xoy 平面内,MN 和 x 轴之间有平行于y 轴的匀强电场和垂直于xoy 平面的匀强磁场。y 轴上离坐标原点4 L 的 A 点处有一电子枪,可以沿+x 方向射出速度为v0 的电子(质量为m,电量为e)。如果电场和磁场同时存在,电子将做匀速直线运动。如果撤去电场,只保留磁场,电子将从x 轴上距坐标原点3 L 的 C 点离开磁场。不计重力的影响,求: ( 1 )磁感应强度B 和电场强度E 的大小和方向; ( 2 )如果撤去磁场,只保留电场,电子将从D 点(图中未标出)离开电场。求D 点的坐标; ( 3 )电子通过D 点时的动能。 练习3.如图所示的平行板器件中,存在相互垂直的匀强磁场和匀强电场,磁场的磁感应强度B1 = 0.40 T,方向垂直纸面向里,电场强度E = 2.0×105 V/m, PQ 为板间中线.紧靠平行板右侧边缘xOy 坐标系的第一象限内,有垂直纸面的正三角形匀强磁场区域,磁感应强度B2 = 0.25 T。一束带电量q = 8.0×10-19 C,质量m = 8.0×10-26 kg 的正离子从P 点射入平行板间,不计重力,沿中线PQ 做直线运动,穿出平行板后从y 轴上坐标为(0, 0.2m)的Q 点垂直y 轴射向三角形磁场区,离子通过x 轴时的速度方向与x 轴正方向夹角为60°。则: ( 1)离子运动的速度为多大?(2)试讨论正三角形区域内的匀强磁场方向垂直纸面向里和垂直纸面向外两种情况下,正三角形磁场区域的最小边长分别为多少?并分别求出其在磁场中运动的时间。 xyO+++++E-----B1PQ AvoCxy 练习4、如图所示...