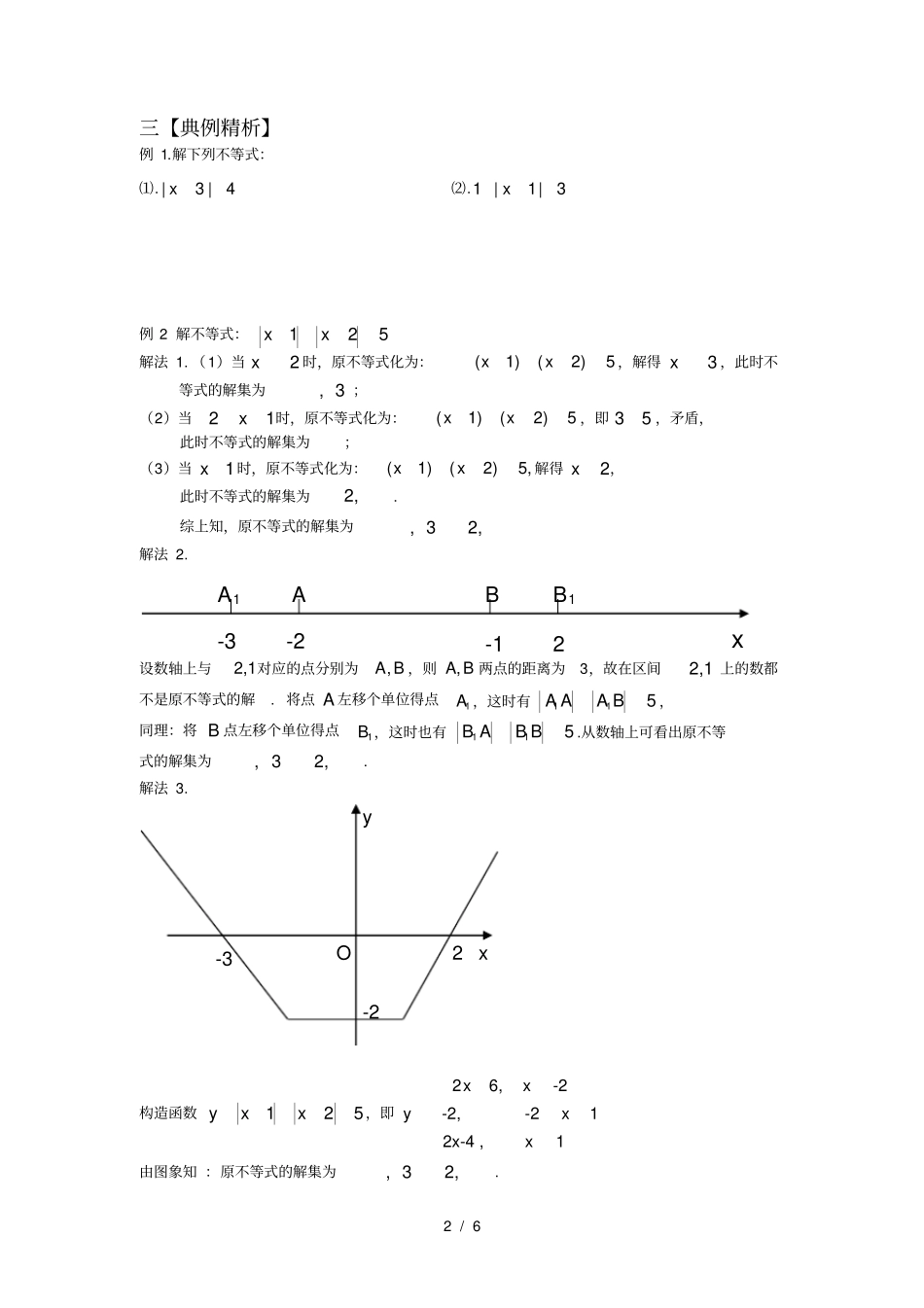
1 / 6 第 6 讲绝对值不等式一【学习目标】1. 理解绝对值的意义;2. 掌握绝对值不等式的解法;3. 掌握绝对值的三角不等式. 二【知识梳理】1. 绝对值的意义(1)绝对值的代数意义:正数的绝对值是它的本身,负数的绝对值是它的相反数,零的绝对值仍是零.即,0,||0,0,,0.aaaaa a(2)绝对值的几何意义:一个数的绝对值,是数轴上表示它的点到原点的距离.两个数的差的绝对值的几何意义:ba表示在数轴上,数a 和数 b 之间的距离.2. 绝对值不等式的解法(1)不等式)0(aax的解集是axax;(2)不等式)0(aax的解集是axaxx或,;(3)不等式)0(ccbax的解集为)0(|ccbaxcx;(4)不等式)0(ccbax的解集为)0(,|ccbaxcbaxx或. 3. 重要 不等式(1) |||||| || ||||ababab ;(2) |||||| || ||||ababab . 4. 区间概念设 ab图示集合区间注: 不等式的解一般用集合或区间表示. A(a) B(b) |a-b| O =a(a>0) A(a) |a| =- a(a<0) |a| A(a) 2 / 6 三【典例精析】例 1.解下列不等式:⑴.4|3| x⑵.3|1|1x例 2 解不等式:125xx解法 1. (1)当2x时,原不等式化为:(1)(2)5xx,解得3x,此时不等式的解集为, 3 ;(2)当21x时,原不等式化为:(1)(2)5xx,即 35 ,矛盾,此时不等式的解集为;(3)当1x时,原不等式化为:(1)(2)5,xx解得2x,此时不等式的解集为2,. 综上知,原不等式的解集为, 32,解法 2. 设数轴上与2,1对应的点分别为,A B ,则,A B 两点的距离为3,故在区间2,1 上的数都不是原不等式的解. 将点 A 左移个单位得点1A ,这时有115A AA B,同理:将 B 点左移个单位得点1B ,这时也有115B AB B.从数轴上可看出原不等式的解集为, 32,. 解法 3. 构造函数125yxx,即26, x-2-2, -2x12x-4 , x1xy由图象知 :原不等式的解集为, 32,.x -12 -2 -3 A B A1B1y x O -3 2 -2 3 / 6 点拨: xaxbcxaxbc和型不等式的解法:①利用绝对值不等式的几何意义②零点分区间③构造函数法例 3.求证: 定理 1:如果 a, b 是实数,则 || ||||,abab当且仅当0ab时,等号成立。证明: 当0ab时,||abab2||()abab222aabb22||2 ||||aabb2(||||)||||abab当0ab时, abab ,2||()abab22222||2 ||||aabbaabb222||2 ||||(||||)||||,aabbabab所以 || ||||,abab当且仅当0ab时,等号成立。点拨: |a|,|b|,|a-b|,|a+b| 之间的关系是:|a|-|b|≤|a+b|, |a|+|b|≥|a-b|, |a|-|b|≤...