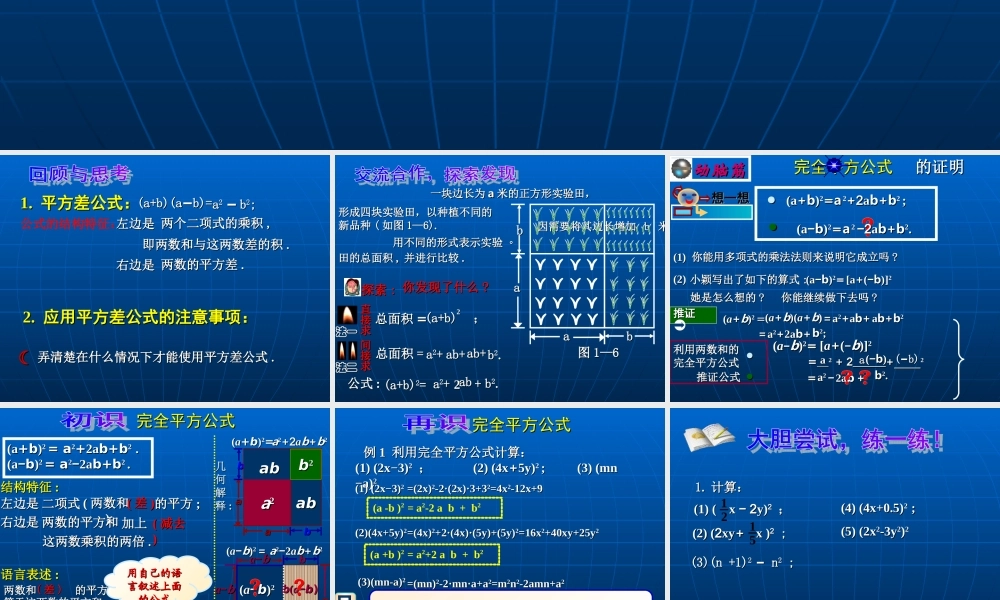
公式的结构特征:左边是左边是aa2 2 −− bb22;; 两个二项式的乘积两个二项式的乘积 , , (a+b)(a(a+b)(a−−b)=b)=即两数和与这两数差的积即两数和与这两数差的积 ..右边是右边是 两数的平方差两数的平方差 ..☾☾ 弄清楚在什么情况下才能使用平方差公式弄清楚在什么情况下才能使用平方差公式 ..1. 1. 平方差公式:平方差公式:2. 2. 应用平方差公式的注意事项:应用平方差公式的注意事项: 一块边长为一块边长为 aa 米的正方形实验田,米的正方形实验田,图图 1—61—6aa 因需要将其边长增加 因需要将其边长增加 b b 米米。。形成四块实验田,以种植不同的形成四块实验田,以种植不同的新品种新品种 (( 如图如图 1—6).1—6). 用不同的形式表示实验用不同的形式表示实验田的总面积田的总面积 , , 并进行比较并进行比较 .. aabbbb法一法一 直直接接求求总面积总面积 ==(a+b) (a+b) ;;22法二法二间间接接求求总面积总面积 == aa22++ aabb++ aabb++ bb22..(a+b)(a+b)22== aa22++ aabb ++ bb22..你发现了什么你发现了什么 ? ? 探索探索 :: 22公式公式 :: 完全平方公式完全平方公式 动脑筋动脑筋(1) (1) 你能用多项式的乘法法则来说明它成立吗你能用多项式的乘法法则来说明它成立吗 ??想一想想一想(a(a++bb))22==aa 22++22aabb++bb2 2 ;;((aa++bb))2 2 ==推证推证 推证推证 ((aa++bb))((aa++bb)) ==aa22++aabb++ aabb++bb22==aa22++2a2abb++bb22;;(2)(2)aa 2 2 −2−2aabb++bb22..小颖写出了如下的算式小颖写出了如下的算式 ::(a(a−−bb))22== [a[a++((−−bb)])]22(a(a−−bb))22==她是怎么想的她是怎么想的 ??利用两数和的利用两数和的完全平方公式完全平方公式 推证公式推证公式 ((aa−−bb))22== [[aa++((−−bb)])]22== 22 + + 22 ++ 22 aaaa((−−bb)) ((−−b)b)==aa222a2abb−−bb22..++你能继续做下去吗你能继续做下去吗 ??的证明的证明 (a(a++bb))2 2 = a= a22++22aabb++bb2 2 ..(a(a−−bb))2 2 = a= a22−−22aabb++bb2 2 ..aaaabbbbaa22ababababbb22结构特征结构特征 ::左边是左边是的平方的平方 ;;二项式二项式右边是右边是(( 两数和 两数和 ))(( 差差 ))((aa++bb))22==aa22 −−aabb−−bb((aa−−bb)) == aa22−2−2aabb++bb22 ..==((aa−−bb))22aa−−bbaa−−bbaaaaaabbbb((aa−−bb))b...