31 双曲线 高三数学复习课件圆锥曲线复习人教大纲版 高三数学复习课件圆锥曲线复习人教大纲版VIP免费

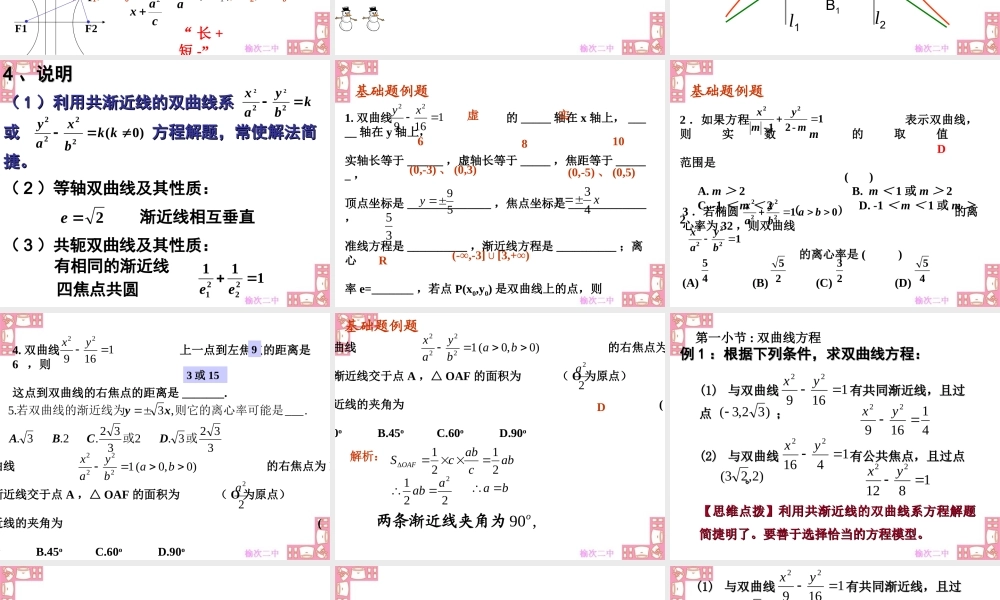
11 、双曲线的、双曲线的定义：定义： 第一定义：第一定义：平面内与两个定点 距离的差平面内与两个定点 距离的差的绝对值等于 的点的轨迹，即点的绝对值等于 的点的轨迹，即点集集21,FF|)|2(221FFaaaPFPFP2|21① ① 时为两射线；时为两射线；② ② 时无轨迹。时无轨迹。③③ 无外面的绝对值则为双曲线一支无外面的绝对值则为双曲线一支 ))212FFa 212FFa 一、基本知识概要：一、基本知识概要：⑵第二定义：平面内到定点 F 的距离和它到一条定直线 l（F 不在 l 上）的距离的比为常数e(e>0)的点的轨迹叫做双曲线. 其中定点 F为双曲线的焦点，定直线 l 为双曲线焦点 F相应的准线. 2 ．双曲线标准方程的两种形式分别表示中心在原点、焦点在 x 轴、 y 轴上的双曲线)0,0(12222babyax)0,0(12222babxay 3 ．双曲线的几何性质：以 表示的双曲线为例，其几何性质如下： )0,0(12222babyaxac(4) 离心率 e= (1,+∞). ∈c=√a2+b2(1) 范围： x≤-a ，或 x≥a(2) 关于 x 轴、 y 轴、原点对称，(3) 两顶点是 (±a,0)(5) 渐近线方程为 y= ，准线方程是 x=xabca2xbayyxabyx渐近线轴焦点在渐近线轴焦点在注;:222222221ababaace (1) 双曲线 右支 上一点 P(x0 ， y0)的左焦半径为 |PF1|=ex0+a ；右焦半径为 |PF2|=ex0-a.(2) 双曲线 左支上一点 P(x0,y0) 的左焦半径为 |PF1|=-ex0-a ，右焦半径为 |PF2|=-ex0+a)0,0(12222babyax)0,0(12222babxayF1F2exaPFaccaxPF||||121PP’“ 长 +短 -”4 ．双曲线的焦半径公式 5. 双曲线 的渐近线方程为 双曲线 的共轭双曲线为)0,0(12222babyax；02222 byax)0,0(12222babyax12222 axby3 、图解双曲线的几何性质oA1A2B1B2F1F2l1l2ＰＭＮ（（ 11 ）利用共渐近线的双曲线系 ）利用共渐近线的双曲线系 或 方程解题，常使解法简或 方程解题，常使解法简捷。捷。 kbyax2222)0(2222kkbxay44 、说明、说明（ 2 ）等轴双曲线及其性质：2e渐近线相互垂直（ 3 ）共轭双曲线及其性质：1112221 ee有相同的渐近线四焦点共圆基础题例题1. 双曲线 的 _____ 轴在 x 轴上， _____ 轴在 y 轴上，实轴长等于 ______ ，虚轴长等于 _____ ，焦距等于 ______ ，顶点坐标是 ______________ ，焦...