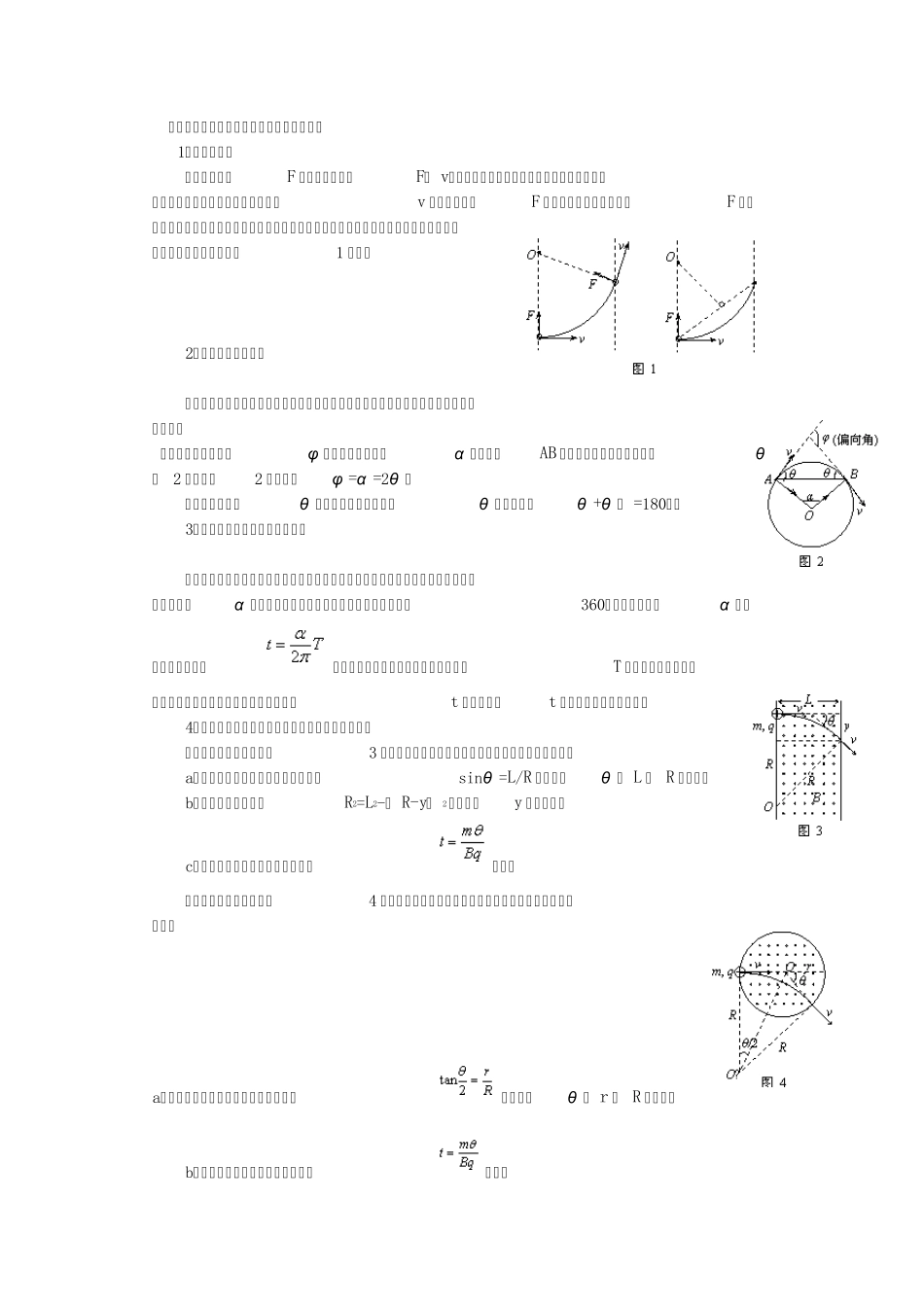
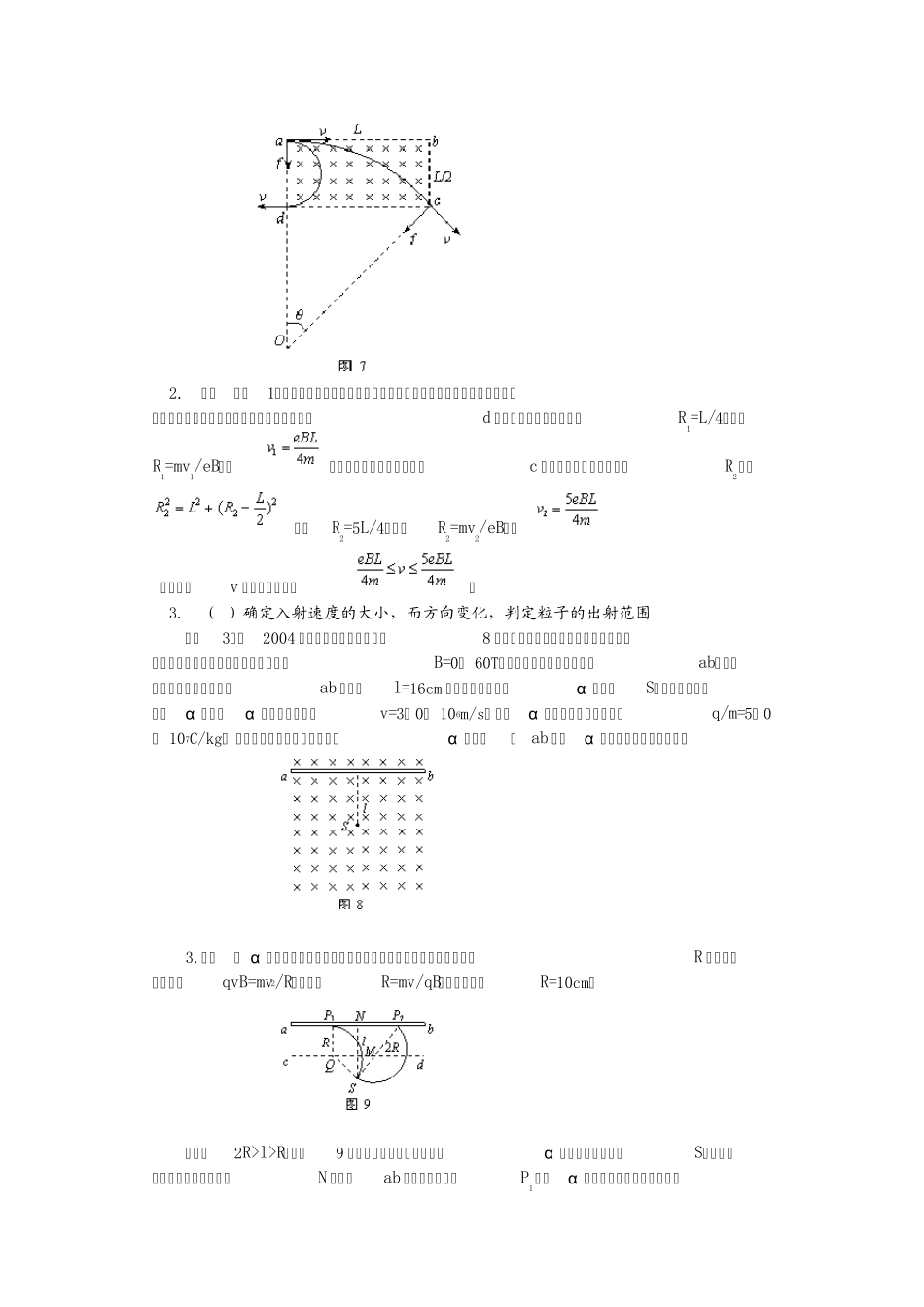
一、带电粒子在有界磁场中运动的分析方法 1.圆心的确定 因为洛伦兹力F 指向圆心,根据F⊥ v,画出粒子运动轨迹中任意两点(一般是射入和射出磁场两点),先作出切线找出v 的方向再确定F 的方向,沿两个洛伦兹力F 的方向画其延长线,两延长线的交点即为圆心,或利用圆心位置必定在圆中一根弦的中垂线上,作出圆心位置,如图1 所示。 2.半径的确定和计算 利用平面几何关系,求出该圆的可能半径(或圆心角),并注意以下两个重要的几何特点: ①粒子速度的偏向角φ 等于转过的圆心角α ,并等于AB 弦与切线的夹角(弦切角)θ的 2 倍,如图2 所示,即φ =α =2θ 。 ②相对的弦切角θ 相等,与相邻的弦切角θ ′互补,即θ +θ ′ =180°。 3.粒子在磁场中运动时间的确定 若要计算转过任一段圆弧所用的时间,则必须确定粒子转过的圆弧所对的圆心角,利用圆心角α 与弦切角的关系,或者利用四边形内角和等于360°计算出圆心角α 的大小,并由表达式,确定通过该段圆弧所用的时间,其中T 即为该粒子做圆周运动的周期,转过的圆心角越大,所用时间t 越长,注意t 与运动轨迹的长短无关。 4.带电粒子在两种典型有界磁场中运动情况的分析 ①穿过矩形磁场区:如图3 所示,一定要先画好辅助线(半径、速度及延长线)。 a、带电粒子在穿过磁场时的偏向角由sinθ =L/R 求出;(θ 、 L 和 R 见图标) b、带电粒子的侧移由R2=L2-( R-y)2解出;(y 见所图标) c、带电粒子在磁场中经历的时间由得出。 ②穿过圆形磁场区:如图4 所示,画好辅助线(半径、速度、轨迹圆的圆心、连心线)。 a、带电粒子在穿过磁场时的偏向角可由求出;(θ 、 r 和 R 见图标) b、带电粒子在磁场中经历的时间由得出。 二、带电粒子在有界磁场中运动类型的分析 1.给定有界磁场 (1)确定入射速度的大小和方向,判定带电粒子出射点或其它 1. 【例1】 ( 2001 年江苏省高考试题)如图5 所示,在y<0 的区域内存在匀强磁场,磁场方向垂直于xy 平面并指向纸面外,磁感应强度为B。一带正电的粒子以速度v0从 O点射入磁场,入射方向在xy 平面内,与x 轴正向的夹角为θ 。若粒子射出磁场时的位置与O 点的距离为l,求该粒子的电量和质量之比q/m。 1.解析:带正电粒子射入磁场后,由于受到洛仑兹力的作用,粒子将沿图6 所示的轨迹运动,从A 点射出磁场,O、 A 间的距离为l,射出时速度的大小仍为v0,射出方...