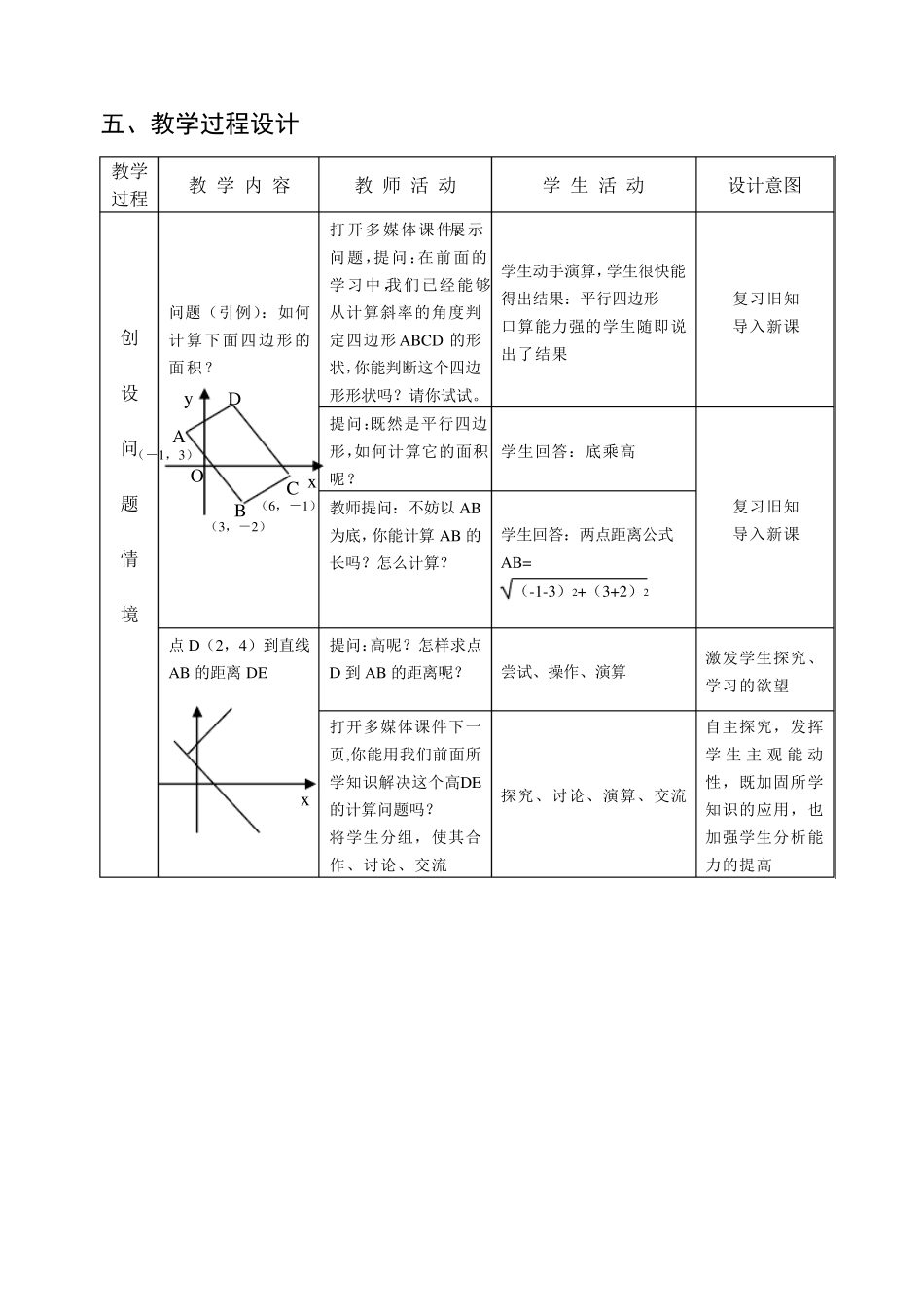
点到直线的距离公式教学设计 一、教材分析 点到直线的距离是直线方程的一个应用,也是坐标法的继续。从知识体系上看,是在研究平面上两点之间距离的基础上来进一步研究点线距离,是对距离度量的完善;从知识结构上看,点到直线的距离是前面讨论两点间距离的深入、后续研究直线和圆的位置关系的准备。 继前面学习了两直线平行与垂直后,教材安排讲述了平面上两点间距离,学生已经基本掌握如何判断四边形形状(包括三角形),以及求四边形边长等方法;为求四边形面积,我们还需探讨点到直线的距离(因为要求四边形中顶点到对边的距离,也包括三角形)。 为此,本课主要研究以下两点:①平面上点到直线的距离公式及其应用;②两条平行线间的距离。 二、教学目标 1 、知识与技能 ①掌握点到直线的距离公式,能应用公式解决一些简单问题; ②通过公式的推导向学生渗透数形结合和化归等数学思想; 2 、过程与方法 ①问题导入的方式; ②分组合作、研究与交流; ③通过对数学公式的推导过程,体会数学中常用的数形结合和化归思想; 3 、情感态度与价值观 ①渗透数形结合和化归等思想,进行对立统一观点的教育,培养学生勇于探索、勇于创新的精神; ②通过数学活动感受数学与显示世界的联系,进一步认识辨证唯物主义的普遍联系观点。 三、教学重难点分析 1 、教学重点 点到直线的距离公式及其应用 2 、教学难点 点到直线距离公式的推导 四、教法构想 在编写过程中,教材将本课设计为一节活动课,通过上一节课的情景,提出问题,进而给出两种解决问题的方法,最后留下思考。因此,教学中可以首先明确条件,提出问题,然后让学生充分讨论,研究如何解决这个问题;将学生分成小组,采用讨论、交流和学生汇报等形式进行研究性学习。 五、教学过程设计 教学过程 教 学 内 容 教 师 活 动 学 生 活 动 设计意图 创 设 问 题 情 境 问题(引例):如何计算下面四边形的面积? 打开多媒体课件,展示问题,提问:在前面的学习中,我们已经能够从计算斜率的角度判定四边形ABCD 的形状,你能判断这个四边形形状吗?请你试试。 学生动手演算,学生很快能得出结果:平行四边形 口算能力强的学生随即说出了结果 复习旧知 导入新课 提问:既然是平行四边形,如何计算它的面积呢? 学生回答:底乘高 复习旧知 导入新课 教师提问:不妨以AB为底,你能计算AB 的长吗?怎么计算? 学生回答:两点距离公式 AB=...