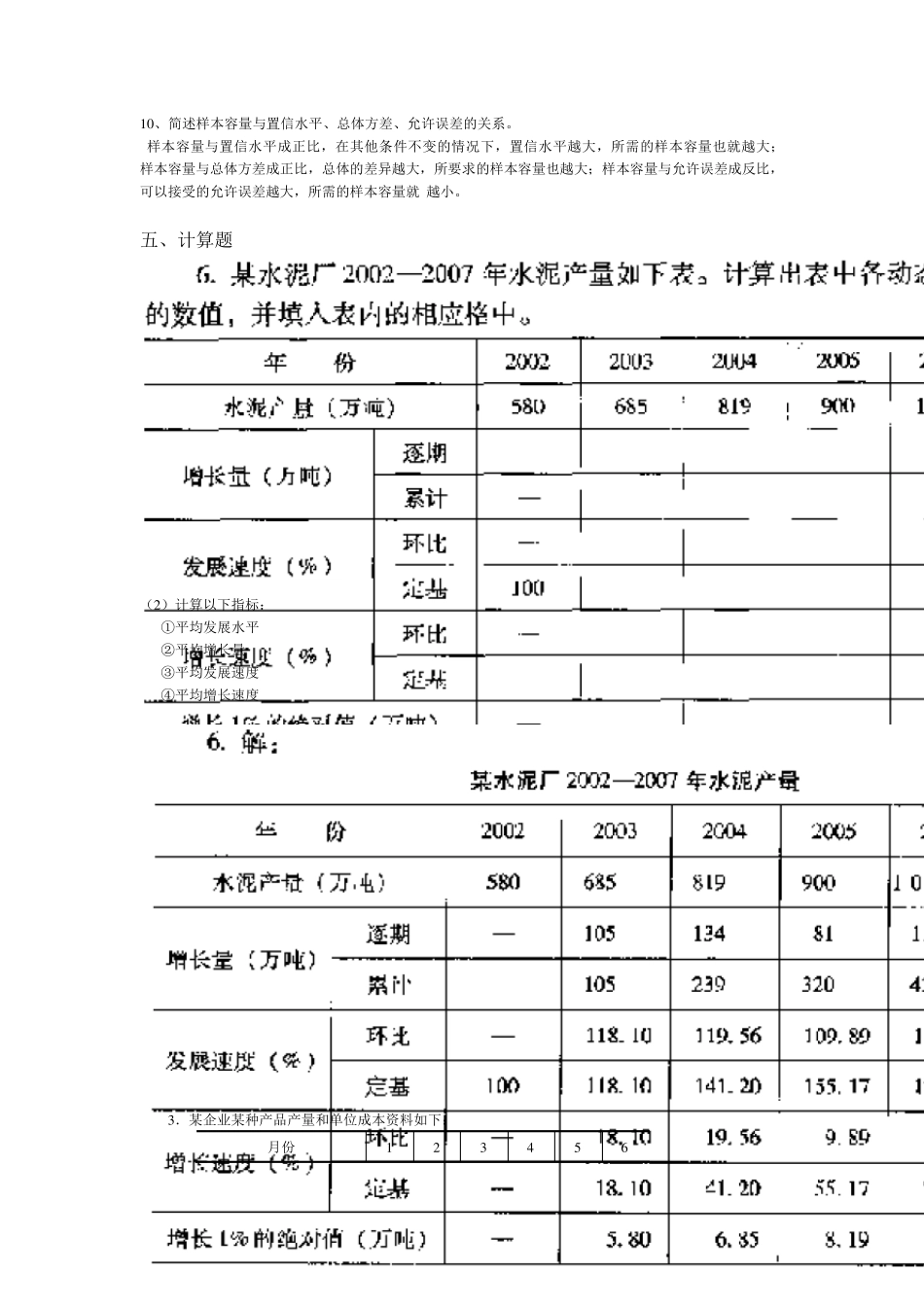
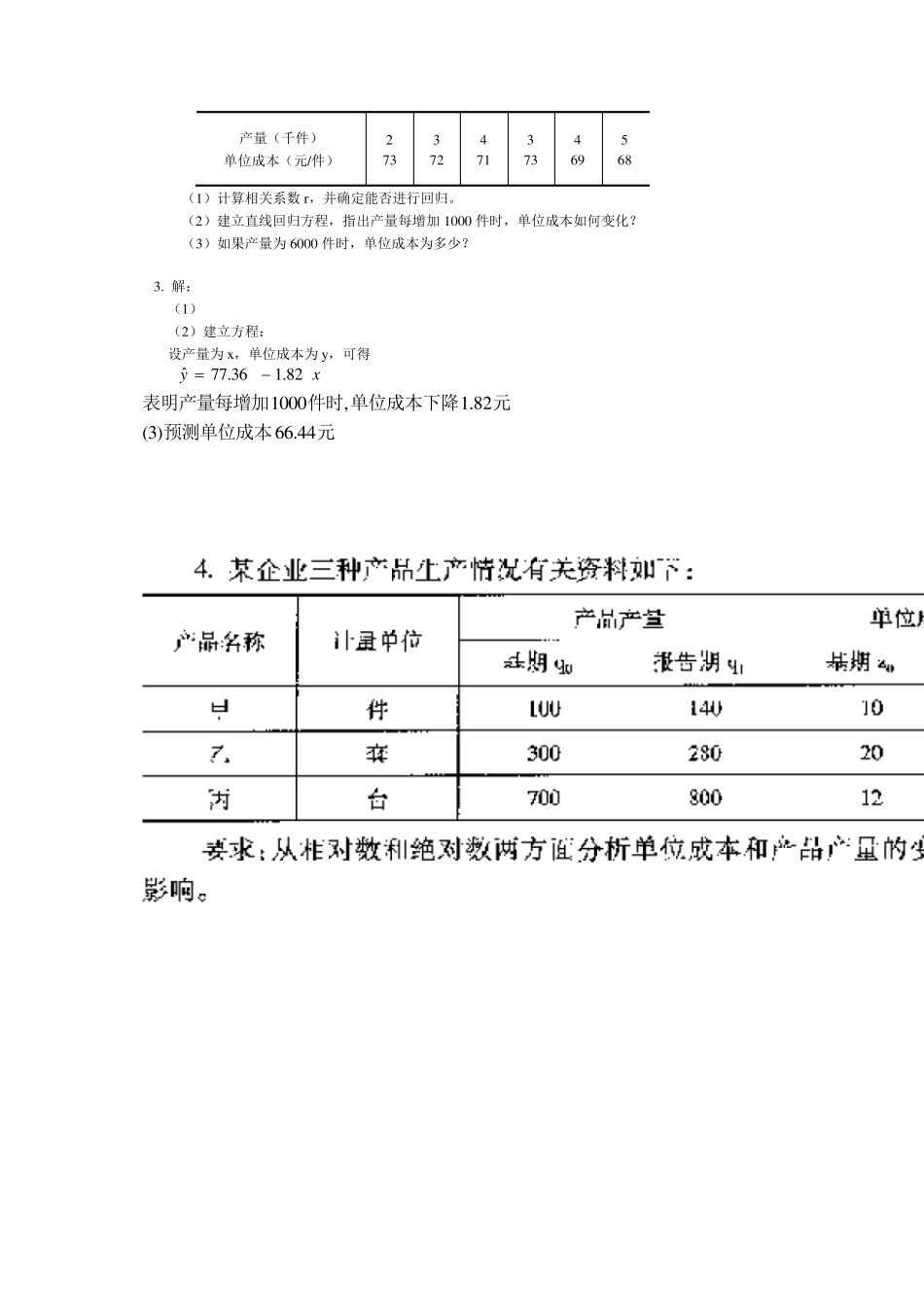
统计学复习题 四、简答题 1、解释总体与样本、参数和统计量的含义。 总体:是人们研究的所有基本单位(通常是人、物体、交易或事件)的总和。 样本:是总体的一部分单位。 参数:描述总体特征的概括性数字度量,它是研究者想要了解的总体的某种特征值。 统计量:根据样本数据计算出来的一个量。 2、解释总体分布、样本分布和抽样分布的含义。 3、简述描述统计学和推断统计学的概念及其联系。 (1)描述统计是用图形、表格和概括性的数字对数据进行描述的统计方法;推断统计是根据样本信息对总体进行估计、假设检验、预测或其他推断的统计方法。(2)两者间联系:一方面反映了统计发展的前后两个阶段,另一方面也反映了统计方法研究和探索客观事物内在数量规律性的先后两个过程。 4、简述中心极限定理。 中心极限定理,是概率论中讨论随机变量和的分布以正态分布为极限的一组定理。这组定理是数理统计学和误差分析的理论基础,指出了大量随机变量之和近似服从正态分布的条件。 5、简述统计工作的过程。 A、统计设计 B 、统计调查 C、统计整理 D、统计分析 6、解释置信水平、置信区间、显著性水平的含义,它们有什么联系。 置信水平:对参数估计的许多置信区间中包含总体参数真值的次数所占比例。置信区间:由样本统计量所构造的总体参数的估计区间。显著性水平:假设检验中犯第一次错误的概率。联系:置信水平越高,置信区间越宽,显著性水平越低。 7、样本统计量的分布和总体分布的关系是什么?影响抽样误差大小的因素有哪些 答:样本统计量包括样本均值、样本比率、样本方差。 (1)样本均值总体分布的关系:①无论是重复还是不重复抽样,样本均值的数学期望始终等于总体均值;②在重复抽样条件下,样本均值的方差为总体方差的 1/n;在不重复抽样条件下,样本均值的方差为1/n (2)样本比率与总体分布的关系:①样本比率p 的数学期望等于总体比率π; ②在重复条件下;在不重复条件下,用修正系数加以修正 (3)样本方差与总体分布的关系:对于来自正态总体的简单随机样本,则比值的抽样分布服从自由度为n-1 的 x²分布。 影响误差:总体各单位标志值的差异程度、样本的单位数、抽样方法和抽样调查的组织形式。 8、简述众数、中位数和均值的特点和应用场合。 答:众数是一组数据中出现数据最多的标志值,它主要是对分类数据的概括性度量,其特点是不受极端值影响,但它没有利用全部数据的信息;中位数是一组数据...