mathematica数学实验报告实验二VIP专享VIP免费

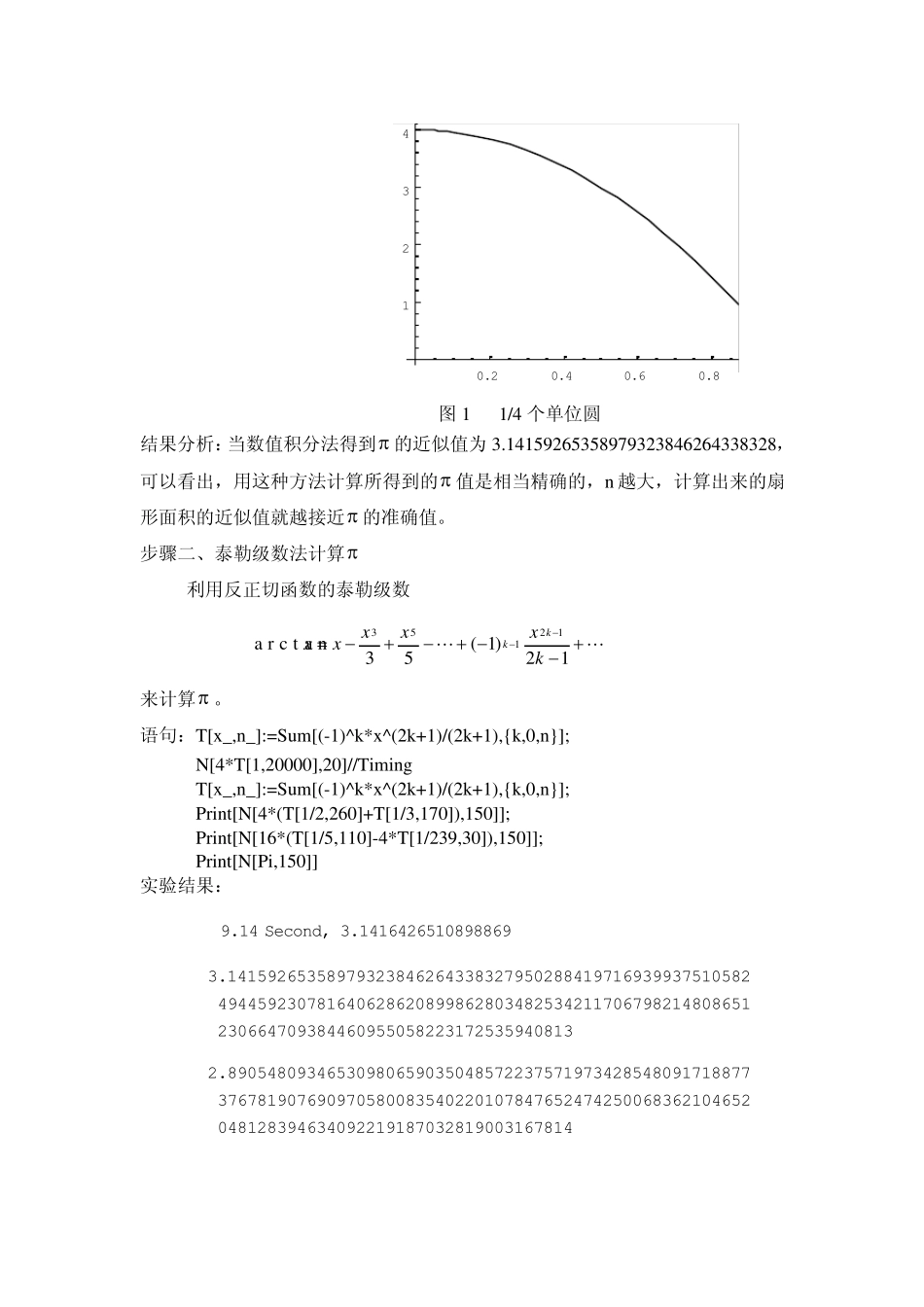
数 学 实 验 报 告 实 验 二 学院：数学与统计学院 班级：信息与计算科学(1)班 姓名： 郝玉霞 学号：201171020107 实验二 一、实验名称：π 的计算 二、实验目的：首先在 Mathematica 环境中用多种方法计算圆周率 的值，通过实验来体会各种方法的区别，比较各种方法的优劣，接着尝试自己提出新的方法来计算圆周率 的值。 三、实验环境：学校机房，Mathematica 软件。 四、实验的基本理论和方法 1、用Mathematica绘图函数Plot绘制圆周率 ； 2、计算圆周率 的数值积分法、泰勒级数法、蒙特卡罗法，并且利用特定的公式来计算圆周率 。 五、实验的内容和步骤及实验的结果和结果分析 步骤一、数值积分法计算 因为单位圆的半径为 1，它的面积等于 ，所以只要计算出单位圆的面积，就算出了 。在坐标轴上画出以圆点为圆心，以 1 为半径的单位圆，则这个单位圆在第一象限的部分是一个扇形，而且面积是单位圆的 1/4，于是，我们只要算出此扇形的面积，便可以计算出 。 当 n=5000 时； 语句： n=5000;y[x_]:=4/(1+x*x); s1=(Sum[y[k/n],{k,1,n-1}]+(y[0]+y[1])/2)/n; s2=(y[0]+y[1]+2*Sum[y[k/n],{k,1,n-1}]+4*Sum[y[(k-1/2)/n],{k,1,n}])/(6*n); Print[{N[s1,20],N[s2,30],N[Pi,30]}]; 实验结果： 3.1415926469231265718, 3.141592653589793238462643343.14159265358979323846264338328 当 n=10000 时； 语句： n=10000;y[x_]:=4/(1+x*x); s1=(Sum[y[k/n],{k,1,n-1}]+(y[0]+y[1])/2)/n; s2=(y[0]+y[1]+2*Sum[y[k/n],{k,1,n-1}]+4*Sum[y[(k-1/2)/n],{k,1,n}])/(6*n); Print[{N[s1,20],N[s2,30],N[Pi,30]}]; Plot[{4(1-x*x)},{x,0,1}] 实验结果： 3.1415926519231265718, 3.141592653589793238462643383.14159265358979323846264338328 0.20.40.60.81234 图1 1/4 个单位圆 结果分析：当数值积分法得到 的近似值为3.14159265358979323846264338328， 可以看出，用这种方法计算所得到的 值是相当精确的，n 越大，计算出来的扇形面积的近似值就越接近 的准确值。 步骤二、泰勒级数法计算 利用反正切函数的泰勒级数 12)1(53a r c t a n12153kxxxxxkk 来计算 。 语句：T[x_,n_]:=Sum[(-1)^k*x^(2k+1)/(2k+1),{k,0,n}]; N[4*T[1,20000],20]//Timing T[x_,n_]:=Sum[(-1)^k*x^(2k+1)/(2k+1),{k,0,n}]; Print[N[4*(T[1/2,2...