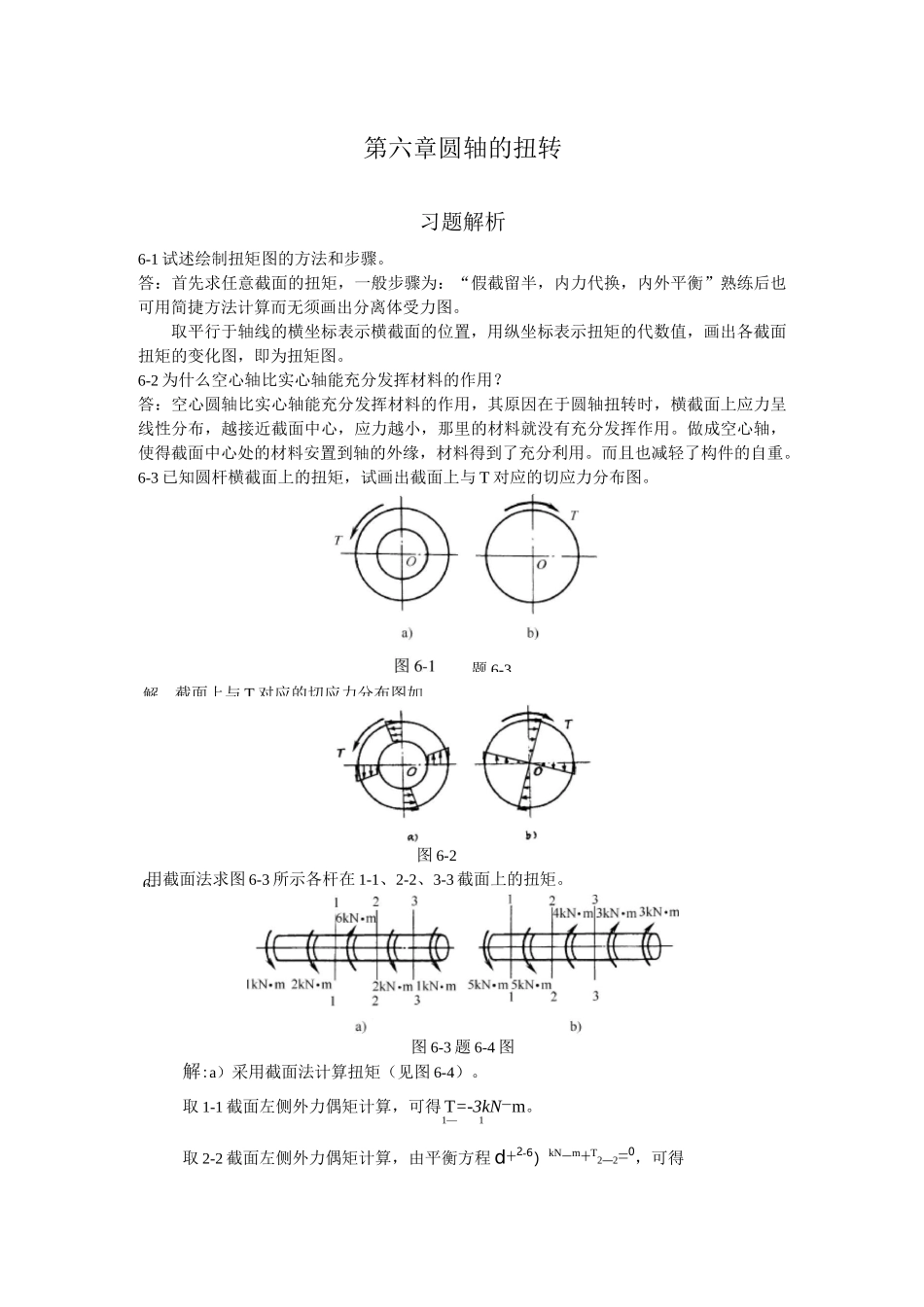
解截面上与 T 对应的切应力分布图如6-第六章圆轴的扭转习题解析6-1 试述绘制扭矩图的方法和步骤。答:首先求任意截面的扭矩,一般步骤为:“假截留半,内力代换,内外平衡”熟练后也可用简捷方法计算而无须画出分离体受力图。取平行于轴线的横坐标表示横截面的位置,用纵坐标表示扭矩的代数值,画出各截面扭矩的变化图,即为扭矩图。6-2 为什么空心轴比实心轴能充分发挥材料的作用?答:空心圆轴比实心轴能充分发挥材料的作用,其原因在于圆轴扭转时,横截面上应力呈线性分布,越接近截面中心,应力越小,那里的材料就没有充分发挥作用。做成空心轴,使得截面中心处的材料安置到轴的外缘,材料得到了充分利用。而且也减轻了构件的自重。6-3 已知圆杆横截面上的扭矩,试画出截面上与 T 对应的切应力分布图。图 6-2用截面法求图 6-3 所示各杆在 1-1、2-2、3-3 截面上的扭矩。图 6-3 题 6-4 图解:a)采用截面法计算扭矩(见图 6-4)。取 1-1 截面左侧外力偶矩计算,可得 T=-3kN-m。1—1取 2-2 截面左侧外力偶矩计算,由平衡方程 d+2-6)kN-m+T2—2=0,可得题 6-3T=3kN・m。2-2取 3-3 截面右侧外力偶矩计算,可得 T 二 1kN・m。3-3IkN-di2hN«mIkN*m2kN*m1kN-m图 6-4b)米用截面法计算扭矩(见图 6-5)。取 1-1 截面左侧外力偶矩计算,可得 T=-5kN・m。i-i取 2-2 截面左侧外力偶矩计算,由平衡方程 6+5)kN・m+T 二 0,可得2-2T=—10kN・m。2-2取 3-3 截面右侧外力偶矩计算,由平衡方程(3+3)kN・m+T=0,可得3-3T=-6kN・m。3-3秋忖・m3kN・EI图 6-56-5 如图 6-6 所示,作各杆的扭矩图。tnbc6kN'bc〕图 6-6 题 6-5 图解:a)采用截面法计算扭矩(见图 6-7)。取 1-1 截面左侧外力偶矩计算,可得:二 4kN-m。取 2-2 截面右侧外力偶矩计算,可得 t 一 2kN-m。作出扭矩图。a)图 6-7b)由力矩平衡方程可得 MA—2M(负号表示与图中假设方向相反)。采用截面法计算扭矩(见图 6-8b)。取 1-1截面左侧外力偶矩计算,可得 Ti_i一 2M。取 2-2 截面右侧外力偶矩计算,可得 T2_2-Me。作出扭矩图。c)由力矩平衡方程可得 MC-0。采用截面法计算扭矩(见图 6&)。取 1-1截面左侧外力偶矩计算,可得 T1_1-M。取 2-2 截面右侧外力偶矩计算,可得°。作出扭矩图。4kN-2kN-.Wt.T2一 M7N-m。绘出的扭矩图如图 6-9所示。1(2)由扭矩图可见 BC 段扭矩最大,由于是等截面圆轴,故危险截面在 ...