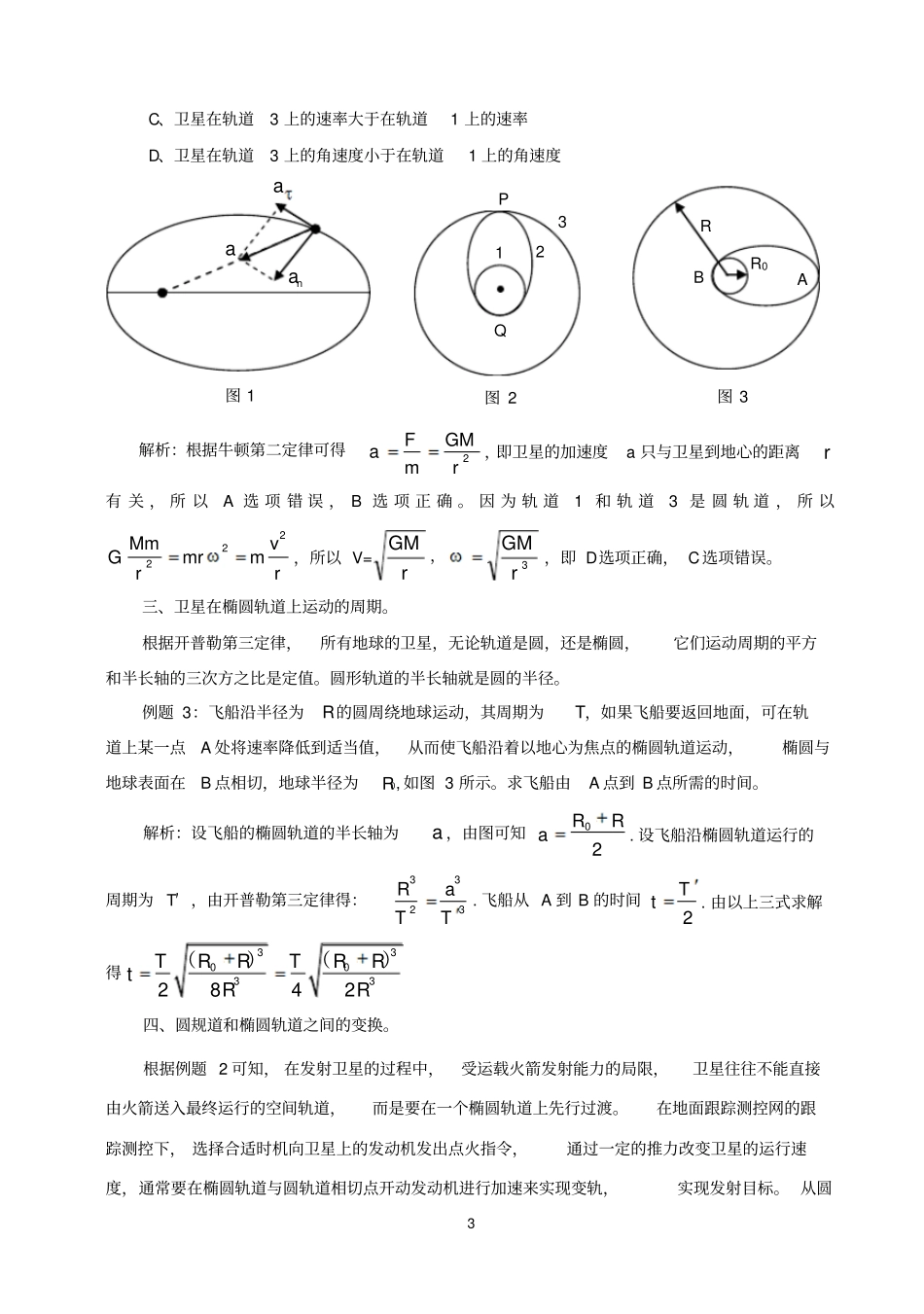
1 卫星椭圆轨道问题探析通过对万有引力知识的学习,我们知道,发射卫星的最小速度是gR (又称第一宇宙速度),此时卫星以最大速度绕地球表面作圆周运动;当发射速度达gR2时(又称第二宇宙速度),卫星以地球球心为焦点作抛物线运动,当然再也不可能返回地球,因为抛物线为非闭合曲线;当发射速度介于gR 和gR2之间时,卫星作椭圆运动,并随发射速度的增大椭圆越扁,地球为椭圆的一个焦点,发射点为近地点;当卫星速度大于gR2而小于第三宇宙速度时, 它将在地球引力范围内作双曲线运动,当卫星脱离地球引力后,将绕太阳运动成为太阳的一个行星, 如果控制发射速度和轨道,它也可成为其它行星的卫星;当发射速度大于第三宇宙速度时,卫星将脱离太阳系的束缚,向其他星系运动。对于圆轨道, 由于卫星受到的万有引力刚好提供卫星运动的向心力,因此可方便地可以求解出卫星在圆轨道上运动的速度、加速度、 周期等物理量。 但对于椭圆轨道,相对来说求解某些问题有一定的困难,下面就卫星椭圆轨道的几个问题逐一分析说明。一、椭圆上任一点的曲率半径。根据数学知识,曲率半径由公式3222)xyry xx y(给出,为了便于求导,借助椭圆的参数方程cosxa,sinyb( a、b 分别为椭圆的半长轴、半短轴),把 x、y 的一、二阶导数代入 r 表达式, 有322222sincos)abrab(.在远地点和近地点,参数 Φ 分别取 0、代入,得到在椭圆上(, 0)a这两个点所在处的曲率半径相同,等于2ba, 不等于 ac 或ac ,式中 c 为椭圆焦距。该知识点中的数学能力要求已超出高中要求,但是其结论有必要作适当的介绍。例题 1:某卫星沿椭圆轨道绕地球运行,近地点离地球中心的距离是c , 远地点离地球中心的距离为 d , 若卫星在近地点的速率为cv , 则卫星在远地点时的速率dv 是多少?解析:做椭圆运动的卫星在近地点和远地点的轨道曲率半径相同,设都等于r 。所以,在近地点时有22cvMmGmcr,在远地点时有22dvMmGmdr,上述两式相比得cdvdvc,故dccvvd。学生易错的解是:卫星运行所受的万有引力提供向心力,在近地点时,有2 22cvMmGmcc,在远地点时有22dvMmGmdd,上述两式相比得cdVdVc,得dccVVd,以上错误在于认为做椭圆运动的卫星,在近地点和远地点的轨道曲率半径不同,且分别为c和 d,这种错误在知道了椭圆曲率半径的概念后就不会犯了。二、卫星在椭圆轨道上运动到任何一点的加速度和向心加速度。根据牛顿第二定律,卫星在椭圆轨道上运动到任何一点...