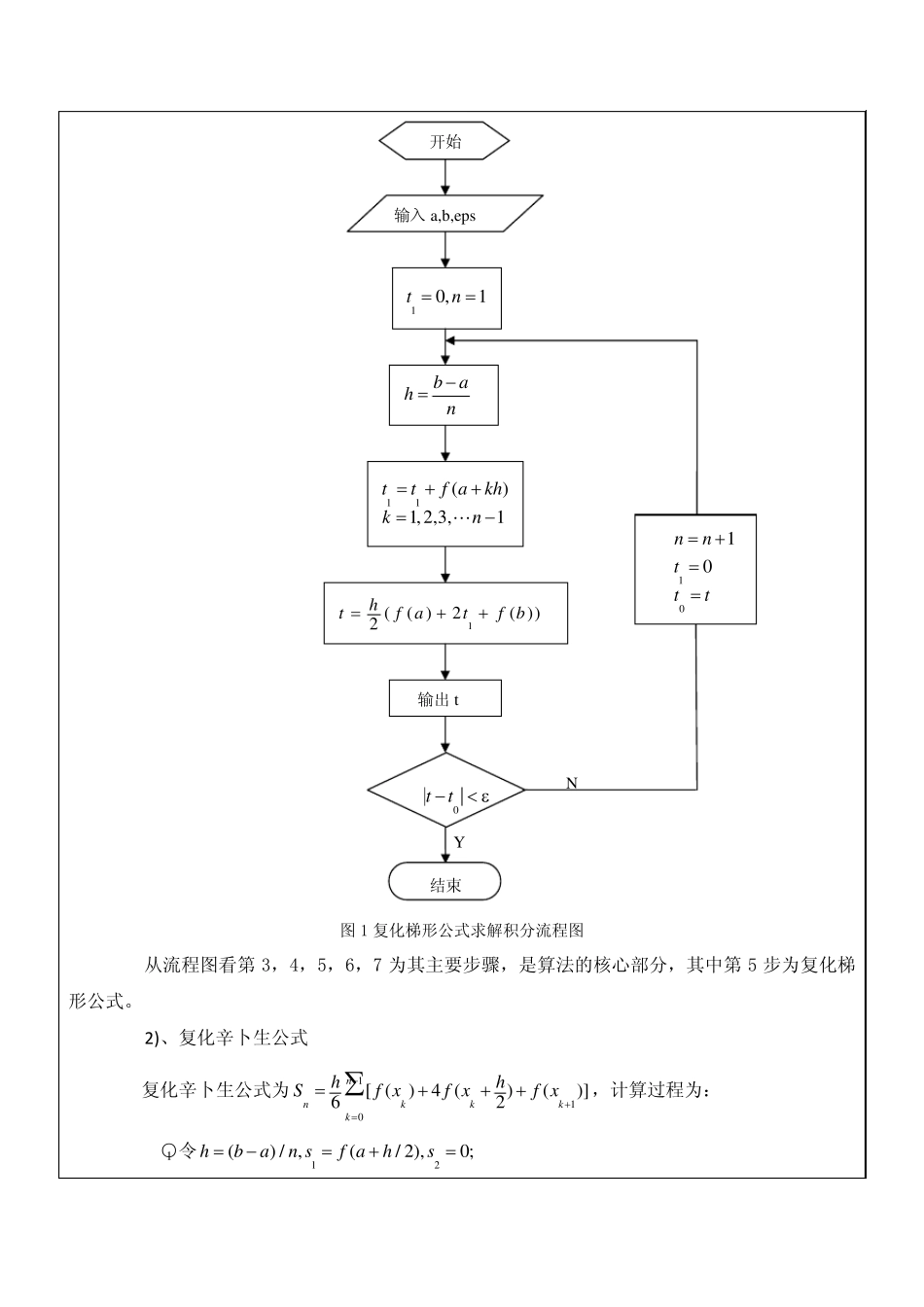
电 子 科 技 大 学 《数值计算方法》 实 验 报 告 学生姓名: 陈文龙 学 号:2 7 0 4 1 0 2 0 1 4 教师:赖生建 一、实验室名称:211 大楼206 室 二、实验项目名称:《数值计算方法》实验6——数值积分 三、实验原理: 1、复化求积公式 复化求积公式是为提高计算的积分精度,把积分区间分为若干个小区间,将所求积分 ( )I f 写成这些小区间上的积分之和,然后对每个小区间上的积分应用柯特斯公式,并把每个小区间上的结果累加即所得为复化柯特斯公式 1)、复化梯形公式 复化梯形公式为110( )[ ()()]2nnkkkhTff xf x−+==+∑或1011( )[ ()2()()]2nnknkTfh f xf xf x−==++∑,计算过程为: ○1 令1() / ,0;hban t=−= ○2 对1,2,,1kn=−"计算 11()ttf akh=++ (1) ○3 1( ( )2( ))2htf atf b=++ (2) 图1 复化梯形公式求解积分流程图 从流程图看第3,4,5,6,7 为其主要步骤,是算法的核心部分,其中第5 步为复化梯形公式。 2 )、复化辛卜生公式 复化辛卜生公式为110[ ()4 ()()]62nnkkkkhhSf xf xf x−+==+++∑,计算过程为: ○1 令12() / ,(/ 2),0;hban sf ahs=−=+= 输入 a,b,eps 0tt−< ε1(( )2( ))2htf atf b=++ bahn−= 1010nnttt=+== 10,1tn==11()1,2,3,1ttf akhkn=++=−"输出 t YN 结束开始 ○2 对1,2,,1kn=−"计算 1122(/ 2),()ssf akhhssf akh=+++=++ (3) ○3 12( ( )42( ))6hsf assf b=+++ (4) 图 2 复化辛卜生公式求解积分流程图 从流程图看第 3,4,5,6,7 为其主要步骤,是算法的核心部分,其中第 5 步为复化辛卜生公式。 输入 a,b,eps 0ss−< ε12( ( )42( ))6hsf assf b=+++bahn−= 12010nnssss=+=== 12(/ 2),0,1sf ahsn=+==1122(/ 2)()1,2,3,1ssf akhhssf akhkn=+++=++=−" 输出 s YN 开始结束3)、复化柯特斯公式 复化柯特斯公式为113424110( )[7 ()32 () 12 ()32 ()7 ()]90nnkkkkkkhCff xf xf xf xf x−++++==++++∑,计算过程为: ○1 令 1234() / ,(/ 4),(/ 2),(3 / 4),0;hban cf ahcf ahcf ahc=−=+=+=+= ○2 对1,2,,1kn=−"计算 11(/ 4)ccf akhh=+++ (5) 22(/ 2)ccf akhh=+++ (6) 33(3 / 4)ccf akhh=+++ (7) 44()ccf akh=++ (8) ○31234(7 ( )321232147 ( ))90hcf accccf b=+++++ (9) 图3 复化柯特斯公式求解积分...