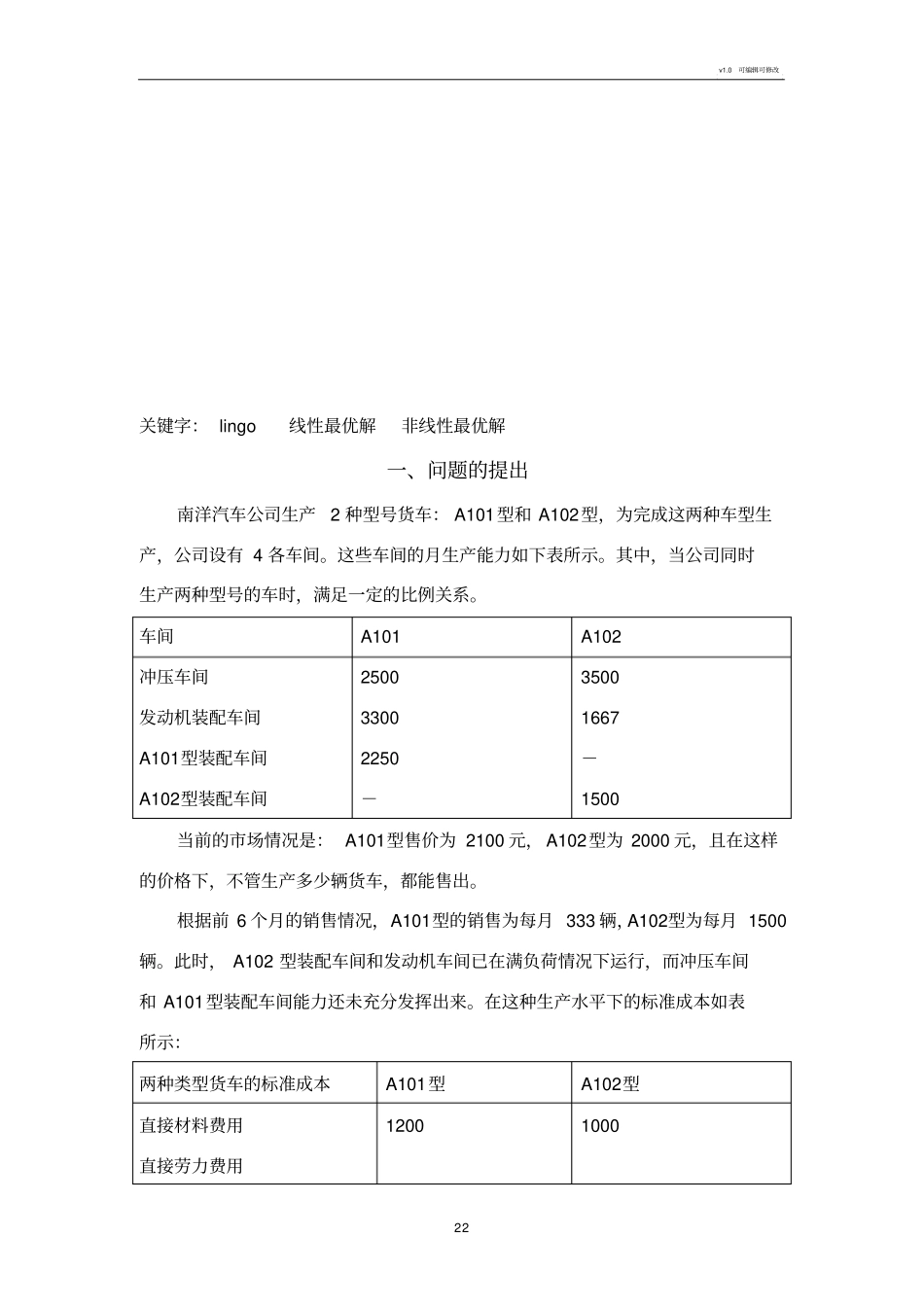
v1.0 可编辑可修改00论文题目: B 题:汽车公司的最佳生产方案队员: 1、10 保险系张康2、10 保险系何嘉欣3、10 保险系袁运接指导教师 :日期: 2011 年 8 月 22 日v1.0 可编辑可修改11汽车公司的最佳生产方案摘要本文主要研究的是在一定资源和生产能力的条件下建立货车公司的最佳生产方案的数学模型。主要方法是利用LINGO软件求一定约束条件下的最优化解。通过对题目的分析,我们建立了模型一,利用lingo软件进行非线性求解,在现有的资源条件下调整两车型的产量得到:当每月生产 2054 辆 A101型车 623辆 A102型车时,则可得到半年最大毛利益为千元。但对模型一检验时发现,模型一将问题繁琐化, 生产甲型和乙型货车显然是受 4 个车间的生产能力限制的,也就是说, 4 个车间每月的生产能力是我们的约束条件;而销售额及产品成本的差价(即毛收益) 才是我们所关心的目标函数,这就将问题转为线性规划的问题。于是建立模型二,运用lingo软件线性规划求解,问题A(1) 在现有的资源条件下调整两车型的产量得到:生产A101车型 2048 辆, 生产 A102型车 632 辆月毛利益为 450600 元。对于 A(2) ,可在模型二的基础上改变约束条件求解得:公司付给其他厂商每辆A101型车的“外包加工费”应不高于元。对于题 B,在模型二的基础上改变发动机车间的劳力费和不变管理费求得:每月生产 A101型货车 1428 辆,A102型货车 1500 辆时,公司半年所得的毛利润为 元,结果并不如合理配置资源好,因此不采用加班的方式。模型二检验出模型一是繁琐的,而模型二程序运行时间很短,算法稳定, 准确性高,容量大,逻辑性严格,计算速度快,具有较强的说服力。最后,我们对模型二的三种生产计划进行了对比分析,并对模型进行评价。v1.0 可编辑可修改22关键字: lingo 线性最优解非线性最优解一、问题的提出南洋汽车公司生产2 种型号货车: A101型和 A102型,为完成这两种车型生产,公司设有 4 各车间。这些车间的月生产能力如下表所示。其中,当公司同时生产两种型号的车时,满足一定的比例关系。车间A101A102冲压车间发动机装配车间A101型装配车间A102型装配车间250033002250-35001667-1500当前的市场情况是: A101型售价为 2100 元, A102型为 2000 元,且在这样的价格下,不管生产多少辆货车,都能售出。根据前 6 个月的销售情况,A101型的销售为每月 333 辆,A102型为每月 1500辆。此时, A102 型装...