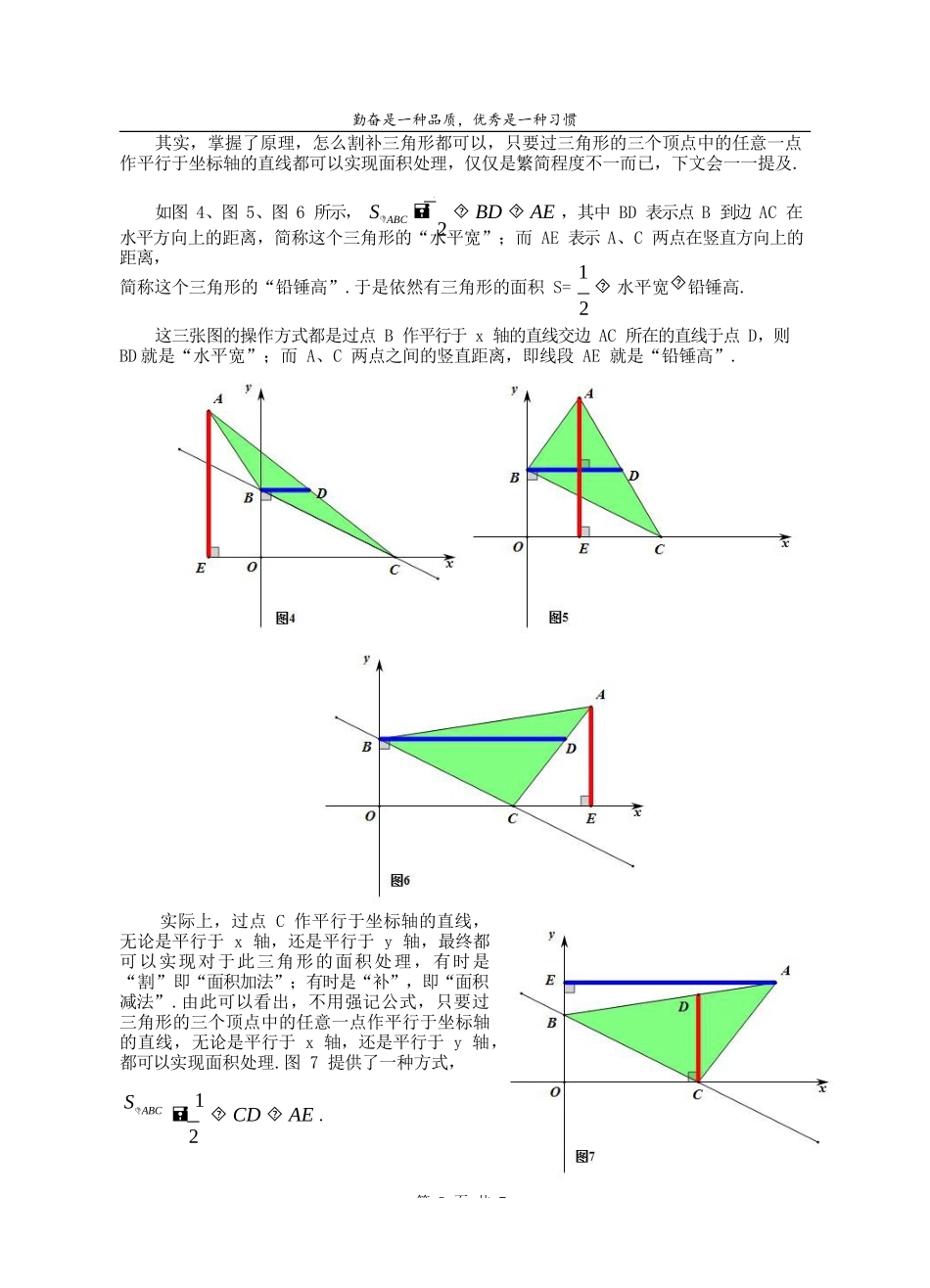
勤奋是一种品质,优秀是一种习惯第 1 页 共 7 三角形面积问题之“宽高公式”的实战分析高邮市赞化学校段广猛《三角形面积问题之“宽高公式”的两种证明方法》一文中,主要介绍了三种情形下 “宽高公式”模型的证明.如图 1、图 2、图 3 所示, SABC 1 OC AD ,其中 OC 表示 B、C 两点在水平方向2上的距离,简称这个三角形的“水平宽”;而 AD 表示点 A 到边 BC 在竖直方向上的距离,简称这个三角形的“铅锤高”.于是三角形的面积 S= 1 水平宽铅锤高,这个公式不妨称2为“宽高公式”.细心观察上面三种情形,操作方式都是过点 A 作平行于 y 轴的直线交边 BC 所在的直线于点 D,则 AD 就是“铅锤高”;而 B、C 两点之间的水平距离,即线段 OC 就是“水平宽”.在实际应用中,笔者不建议学生固化思维,强记这里的结论而直接使用.一方面,这个公式课本上并没有直接出现,中考时能不能直接使用值得商榷;另一方面,对于图 2 的结论,大部分学生普遍可以接受,但是若是不知道这个公式推导的来龙去脉而强行直接使用,图 1 及图 3 的结论,多数学生是很难理解原理而导致不能正确使用.更何况,这三种情形下的推导过程也是相辅相成、思想统一的,都采用了“改斜归正”及“割补法”的思想,而这两种思想方法又是极其重要的解题原理,需要同学们认真深刻体会的,所以笔者强烈建议学生体会这里的推导原理,以达到灵活使用的目的.1勤奋是一种品质,优秀是一种习惯第 2 页 共 7 其实,掌握了原理,怎么割补三角形都可以,只要过三角形的三个顶点中的任意一点作平行于坐标轴的直线都可以实现面积处理,仅仅是繁简程度不一而已,下文会一一提及.如图 4、图 5、图 6 所示, SABC 2 BD AE ,其中 BD 表示点 B 到边 AC 在水平方向上的距离,简称这个三角形的“水平宽”;而 AE 表示 A、C 两点在竖直方向上的距离,简称这个三角形的“铅锤高”.于是依然有三角形的面积 S= 1 水平宽铅锤高.2这三张图的操作方式都是过点 B 作平行于 x 轴的直线交边 AC 所在的直线于点 D,则 BD 就是“水平宽”;而 A、C 两点之间的竖直距离,即线段 AE 就是“铅锤高”.实际上,过点 C 作平行于坐标轴的直线,无论是平行于 x 轴,还是平行于 y 轴,最终都可以实现对于此三角形的面积处理,有时是“割”即“面积加法”;有时是“补”,即“面积减法”....