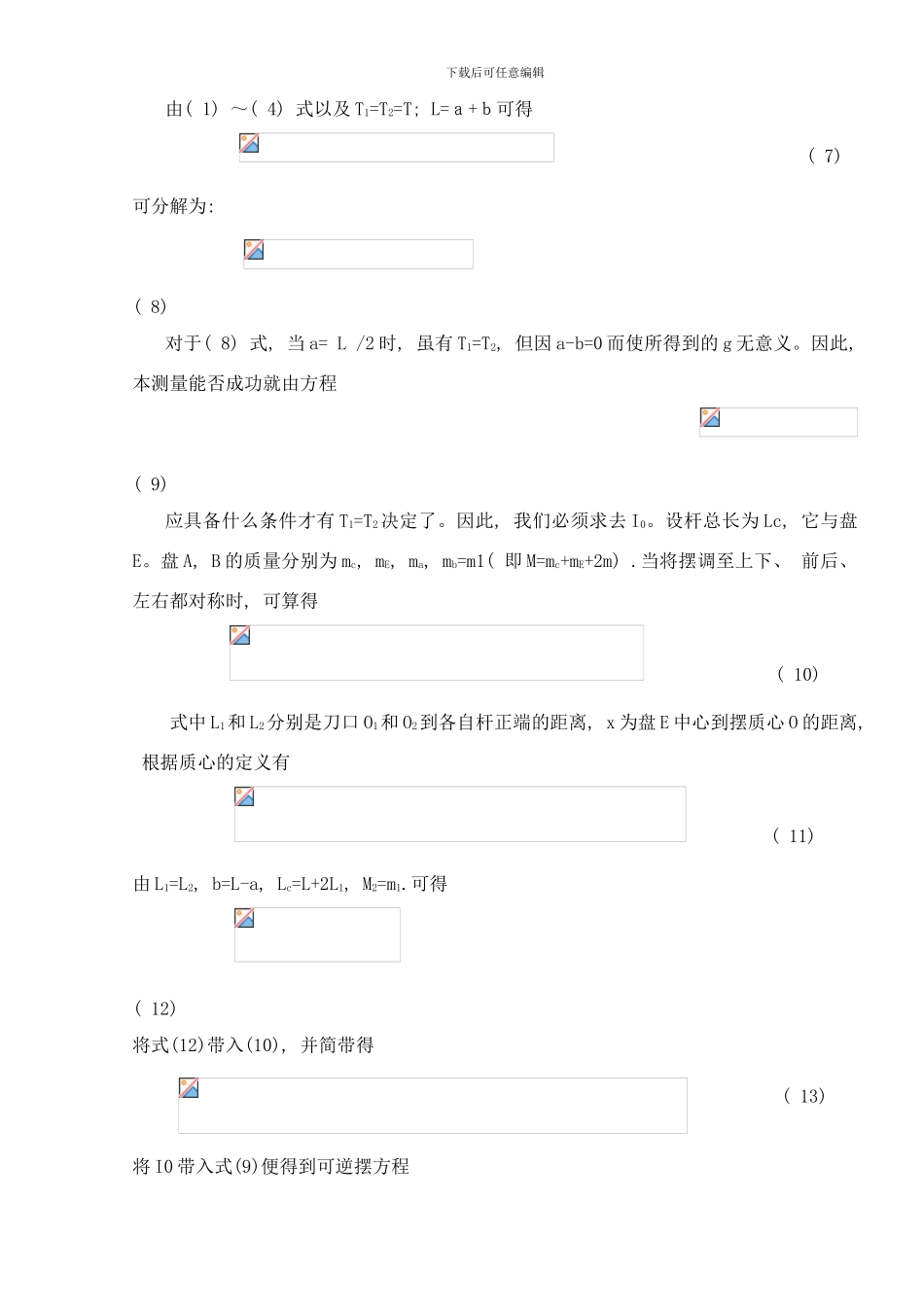
下载后可任意编辑可逆摆运动特性的讨论刘勇( 安庆师范学院物理与电气工程学院 安徽 安庆 246011) 指导老师: 张 杰摘要: 本文根据可逆摆的物理图象和运动学方程, 建立了可逆摆的目标函数和控制数学模型。经过对目标函数控制物理机理的讨论, 寻找目标函数的极值, 然后利用MATLAB 的 Simulink 进行了可逆摆的运动学仿真。在仿真过程中我们应用全维状态观测设计控制器实现了状态反馈, 在此基础上用状态反馈控制配置系统极点, 能够在最短的时间内寻找到系统的平衡位置。仿真结果表明, 该方法可使系统稳定工作并具有良好的动态性能, 并能较好地解释可逆摆实验中一系列物理现象。这为我们提供了一种利用状态反馈进行控制系统优化的手段。关键词: 可逆摆, 状态反馈, MATLAB, 自动控制, 仿真1.引言北京大学赵凯华教授指出[1]: ”物理学家对事物是最好穷本极源的, 她们在讨论的过程中不段地思考, 凡事总喜爱问个‘为什么’。理论物理学家不能仅仅埋首于公式的推演, 应该询问其物理实质, 从中构想出鲜亮的无论图象来; 实验物理学家不应满足于现象和数据的记录, 或某种先进的指标, 而要追究其中的物理机理”。可逆摆问题在控制理论的讨论中是一个很典型的范例 [2-3]。本文根据可逆摆运动学方程, 建立可逆摆目标函数的物理图象, 分析( L-x) 图象的形成机理, 讨论可逆摆上的大锤对目标函数控制的物理机理, 从而较好地解释了可逆摆实验中一系列物理现象。2.可逆摆原理及运动方程2.1 可逆摆的振动周期在大学实验教材中, 可逆摆是一种可倒过来摆动的物理摆[4], 实验原理如图 1, 它是均匀钢体 C 上装有 2 个均匀且平整的钢盘 A 和 B, 杆 C 穿过钢盘, 且穿过盘心。O1, O2为杆 C 的两刀口, 当可逆摆正挂做摆角很小的摆动时, 它做简谐振动, 其周期为图 1 可 逆摆下载后可任意编辑 ( 1) 式中 I1为摆在此时的转动惯量, M 为摆的总质量, a 为刀口 O1到质心 O 的距离。为了消去难于测量 I1与 a, 需保持整个摆的结构不变而仅将摆倒过来绕 O2( 称作倒摆) 摆动则其周期为 ( 2) 式中 I2为摆此时的转动惯量, b 为刀口 O2到摆质心 O 的距离, 两者也难于侧准, 为了消去 I1, I2, a, b, 再用平行轴定理 ( 3 ) ( 4) 则由(1)、 (2)、 (3)、 (4)可得 ( 5) 式中 a, b 虽然难于测量准, 但 a+b 是两刀口之间的距离, 可测得足够准确, 因此, 当条件满足 T1= T2= ...