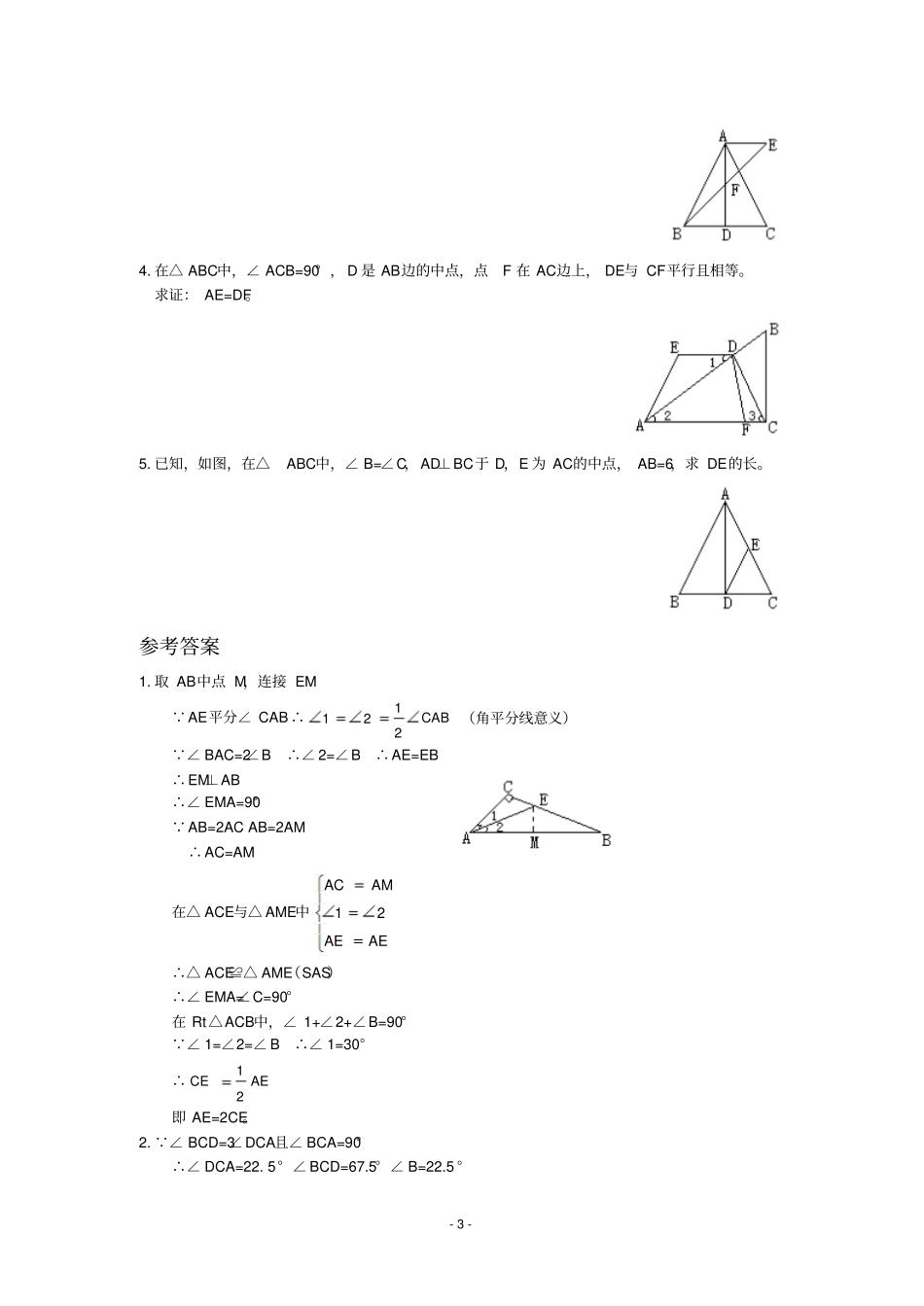
- 1 - 直角三角形的性质重难点重点 :直角三角形的性质定理及其推论:①直角三角形的性质,在直角三角形中,斜边上的中线等于斜边的一半; ②推论:(1)在直角三角形中,如果一个锐角等于30° ,则它所对的直角边等于斜边的一半 ; (2)在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角为30°. 难点:1. 性质定理的证明方法. 2. 性质定理及其推论在解题中的应用. 讲一讲例 1 :已知, Rt△ ABC中,∠ ACB=90° , AB=8cm,D为 AB中点, DE⊥AC于 E,∠A=30° ,求 BC,CD和 DE的长分析 :由 30° 的锐角所对的直角边为斜边的一半,BC可求,由直角三角形斜边中线的性质可求 CD. 在 Rt△ADE中,有∠ A=30° ,则 DE可求 . 解: 在 Rt △ABC中 ∠ ACB=90 ∠A=30° ∴ABBC21 AB=8 ∴BC=4 D为 AB中点, CD为中线∴421ABCD DE⊥AC,∴∠ AED=90°在 Rt△ADE中,ADDE21,ABAD21∴241ABDE例 2 :已知:△ ABC中, AB=AC=BC (△ ABC为等边三角形) D为 BC边上的中点,DE⊥AC于 E. 求证:ACCE41. 分析: CE在 Rt△DEC中,可知是CD的一半,又 D 为中点,故CD为 BC上的一半,因此可证 . 证明: DE⊥ AC于 E,∴∠ DEC=90° ( 垂直定义 ) △ ABC为等边三角形,∴AC=BC ∠C=60° 在 Rt△ EDC中,∠ C=60° ,∴∠ EDC=90° -60 ° =30°∴CDEC21 D为 BC中点,- 2 - ∴BCDC21∴ACDC21∴ACCE41. 例 3 :已知:如图AD∥BC,且 BD⊥CD, BD=CD, AC=BC. 求证: AB=BO. 分析: 证 AB=BD只需证明∠ BAO=∠BOA 由已知中等腰直角三角形的性质,可知BCDF21。由此,建立起AE与 AC之间的关系,故可求题目中的角度,利用角度相等得证. 证明:作DF⊥BC于 F, AE⊥BC于 E △ BDC中,∠ BDC=90° , BD=CD ∴BCDF21 BC=AC ∴ACDF21 DF=AE ∴ACAE21∴∠ ACB=30° ∠ CAB=∠ABC,∴∠ CAB=∠ABC=75°∴∠ OBA=30°∴∠ AOB=75°∴∠ BAO=∠BOA ∴AB=BO 练一练1. △ ABC中,∠ BAC=2∠B,AB=2AC,AE平分∠ CAB。求证: AE=2CE。2. 已知, Rt△ABC中,∠ ACB=90° , CD⊥AB,CE为 AB边上的中线,且∠BCD=3∠ DCA。求证: DE=DC。3. 如图: AB=AC,AD⊥BC于 D,AF=FD,AE∥BC且交 BF 的延长线于E,若 AD=9, BC=12,求BE 的长。- 3 - 4. 在△ ABC中,∠ ACB=90° , D 是 AB边...