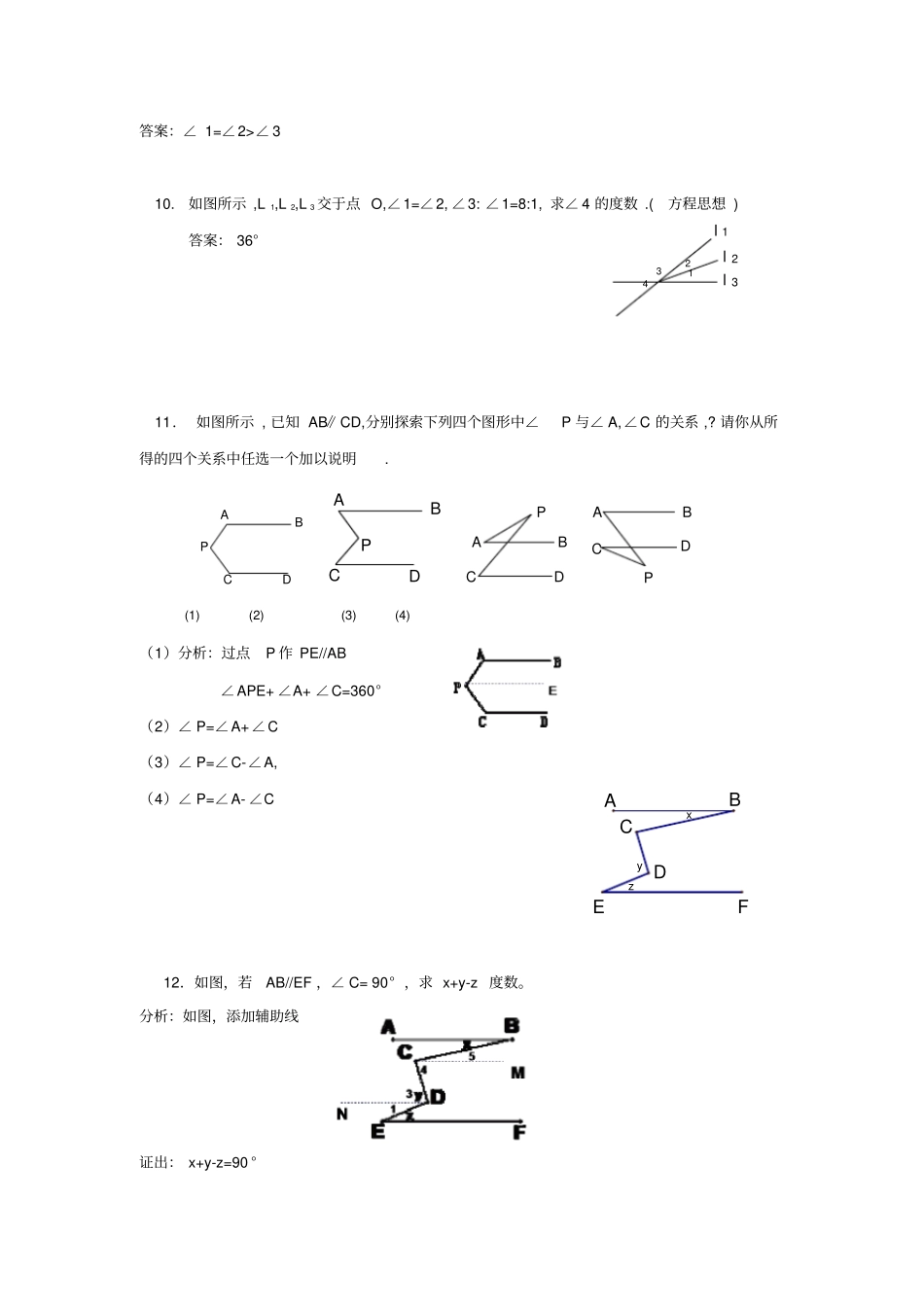
DCBA相交线与平行线一、知识框架相交线两条直线相交邻补角、对顶角对顶角相等两条直线被第三条直线所截同位角、内错角、同旁内角平行线平行公理平移判定性质垂线及性质点到直线的距离二、典型例题1. 下列说法正确的有( B ) ①对顶角相等 ; ②相等的角是对顶角; ③若两个角不相等, 则这两个角一定不是对顶角; ④若两个角不是对顶角, 则这两个角不相等. A.1个 B.2个 C.3个 D.4个2. 如图所示 , 下列说法不正确的是( D ) A.点 B 到 AC的垂线段是线段AB; B.点 C到 AB的垂线段是线段AC C.线段 AD是点 D到 BC的垂线段 ; D.线段 BD是点 B 到 AD的垂线段3. 下列说法正确的有( C ) ①在平面内 , 过直线上一点有且只有一条直线垂直于已知直线; DCBAGFEDCBA12FEDCBAl3l2l1 O②在平面内 , 过直线外一点有且只有一条直线垂直于已知直线; ③在平面内 , 过一点可以任意画一条直线垂直于已知直线; ④在平面内 , 有且只有一条直线垂直于已知直线. A.1个 B.2个 C.3个 D.4个4.一学员驾驶汽车,两次拐弯后,行驶的方向与原来的方向相同,这两次拐弯的角度可能是( A ) A. 第一次向左拐30° 第二次向右拐30° B. 第一次向右拐50° 第二次向左拐130° C. 第一次向右拐50° 第二次向右拐130° D. 第一次向左拐50° 第二次向左拐130°5.如图,若AC⊥BC于 C,CD⊥AB于 D,则下列结论必定成立....的是( C )A. CD>AD B.ACBD D. CD∠ 3 10. 如图所示 ,L 1,L 2,L 3 交于点 O,∠1=∠2, ∠3: ∠1=8:1, 求∠ 4 的度数 .( 方程思想 ) 答案: 36°11. 如图所示 , 已知 AB∥CD,分别探索下列四个图形中∠P 与∠ A,∠C 的关系 ,? 请你从所得的四个关系中任选一个加以说明.PDCBAPDCBAPDCBAPDCBA (1) (2) (3) (4) (1)分析:过点P 作 PE//AB ∠APE+ ∠A+ ∠C=360°(2)∠ P=∠A+∠C (3)∠ P=∠C-∠A, (4)∠ P=∠A- ∠C 12.如图,若AB//EF ,∠ C= 90° ,求 x+y-z 度数。分析:如图,添加辅助线证出: x+y-z=90 °A B 1 E F 2 C P D 13.已知:如图,BAPAPD18012,求证:EF分析:法一法二:由 AB//CD 证明PAB=APC,所以EAP=APF 所以 AE//FP 所以EF