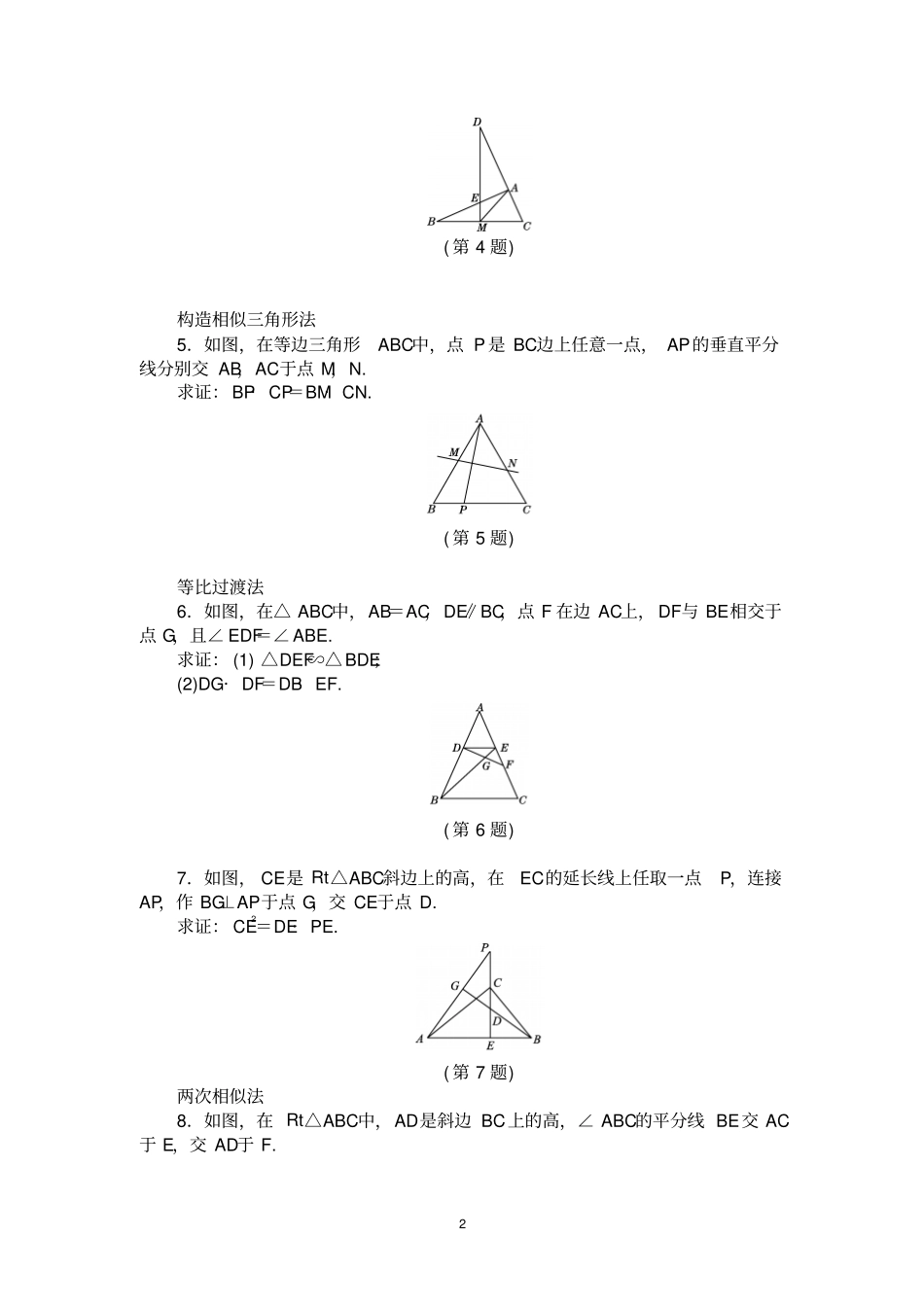
1 相似 专项训练专训 1证比例式或等积式的技巧名师点金:证比例式或等积式,若所遇问题中无平行线或相似三角形,则需构造平行线或相似三角形,得到成比例线段;若比例式或等积式中的线段分布在两个三角形或不在两个三角形中,可尝试证这两个三角形相似或先将它们转化到两个三角形中再证两三角形相似,若在两个明显不相似的三角形中,可运用中间比代换.构造平行线法1.如图,在△ ABC中,D为 AB的中点, DF交 AC于点 E,交 BC的延长线于点 F,求证: AE· CF=BF· EC.( 第 1 题) 2.如图,已知△ ABC的边 AB上有一点 D,边 BC的延长线上有一点E,且 AD=CE,DE交 AC于点 F,试证明: AB· DF=BC· EF.( 第 2 题) 三点找三角形相似法3.如图,在 ?ABCD中,E 是 AB延长线上的一点, DE交 BC于 F. 求证: DCAE=CFAD. ( 第 3 题) 4.如图,在△ ABC中,∠ BAC=90° , M为 BC的中点, DM⊥BC交 CA的延长线于 D,交 AB于 E. 求证: AM2=MD· ME.2 ( 第 4 题) 构造相似三角形法5.如图,在等边三角形ABC中,点 P 是 BC边上任意一点, AP的垂直平分线分别交 AB,AC于点 M,N. 求证: BP· CP=BM· CN.( 第 5 题) 等比过渡法6.如图,在△ ABC中,AB=AC,DE∥BC,点 F 在边 AC上, DF与 BE相交于点 G,且∠ EDF=∠ ABE. 求证: (1) △DEF∽△ BDE;(2)DG· DF=DB· EF.( 第 6 题) 7.如图, CE是 Rt△ABC斜边上的高,在EC的延长线上任取一点P,连接AP,作 BG⊥AP于点 G,交 CE于点 D. 求证: CE2=DE· PE.( 第 7 题) 两次相似法8.如图,在 Rt△ABC中,AD是斜边 BC上的高,∠ ABC的平分线 BE交 AC于 E,交 AD于 F. 3 求证: BFBE=ABBC. ( 第 8 题) 9.如图,在 ?ABCD中,AM⊥BC,AN⊥CD,垂足分别为 M,N.求证:(1) △AMB∽△ AND;(2) AMAB=MNAC. ( 第 9 题) 等积代换法10.如图,在△ ABC中,AD⊥BC于 D,DE⊥AB于 E,DF⊥AC于 F. 求证: AEAF=ACAB. ( 第 10 题) 等线段代换法11.如图,等腰△ ABC中,AB=AC,AD⊥BC于点 D,点 P 是 AD上一点, CF∥AB,延长 BP交 AC于点 E,交 CF于点 F,求证: BP2=PE· PF.4 ( 第 11 题) 12.已知:如图, AD平分∠ BAC,AD的垂直平分线EP交 BC的延长线于点P. 求证: PD2=PB· PC.( 第 12 题) 专训 2巧用“基本图...