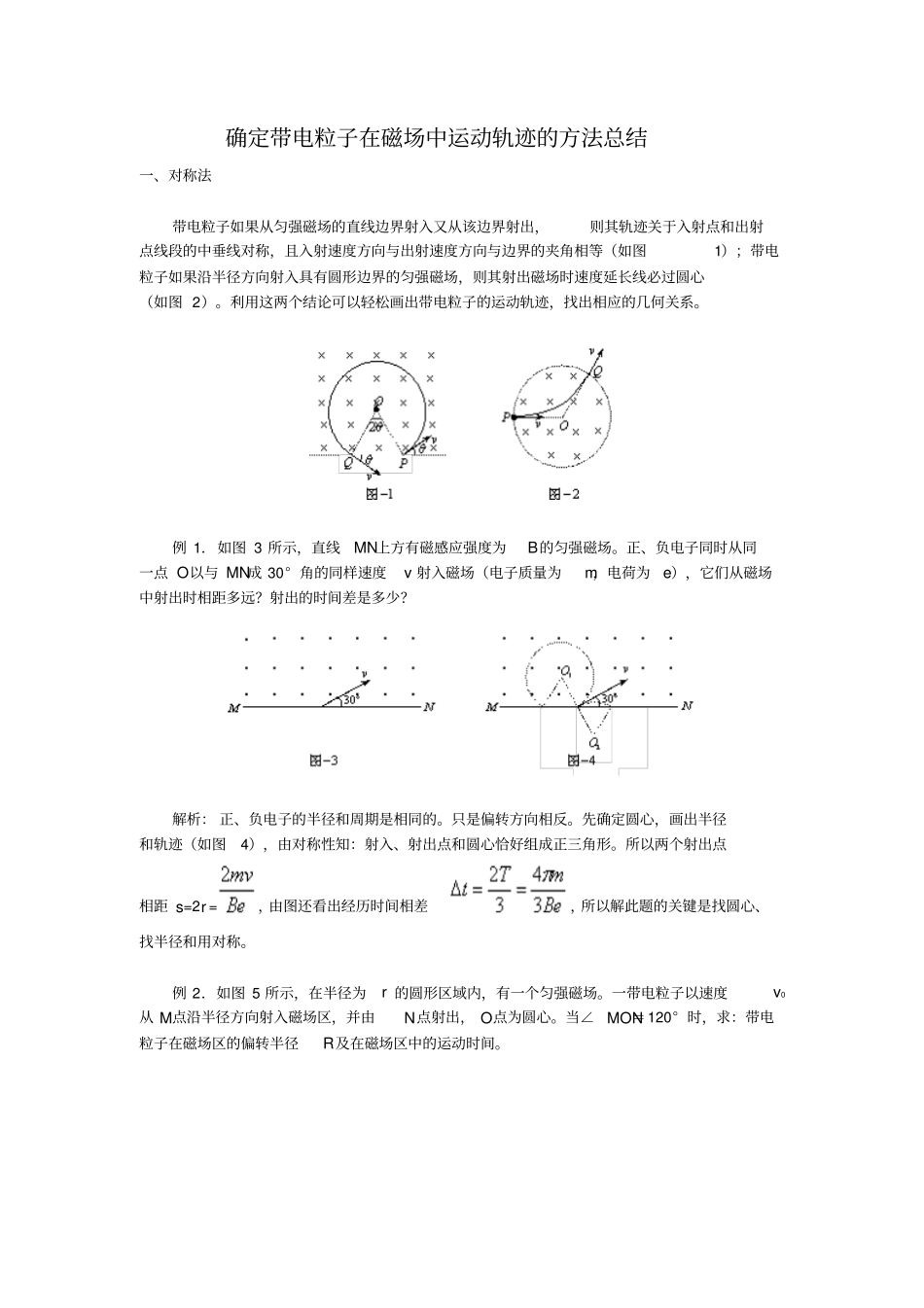
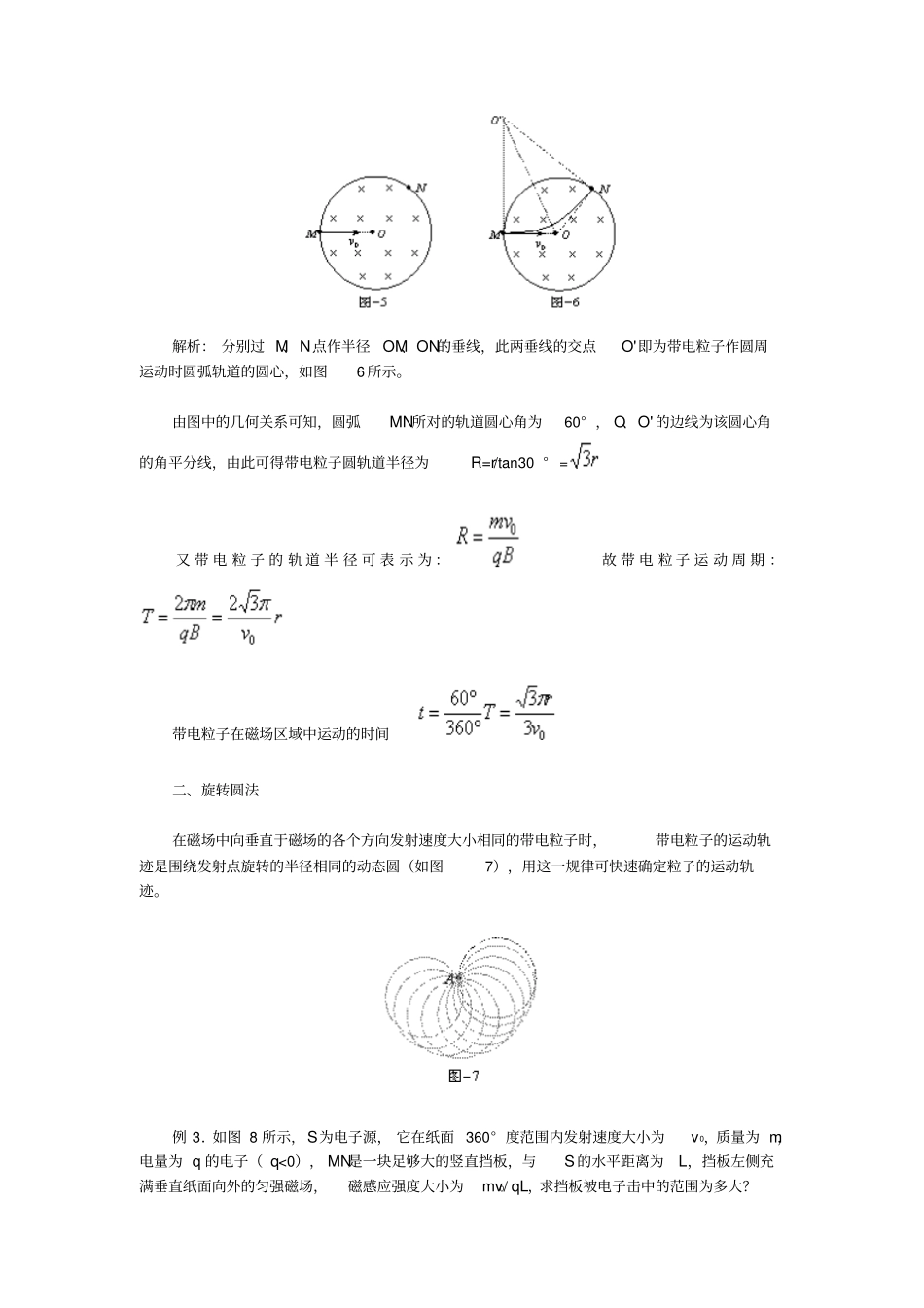
确定带电粒子在磁场中运动轨迹的方法总结一、对称法带电粒子如果从匀强磁场的直线边界射入又从该边界射出,则其轨迹关于入射点和出射点线段的中垂线对称,且入射速度方向与出射速度方向与边界的夹角相等(如图1);带电粒子如果沿半径方向射入具有圆形边界的匀强磁场,则其射出磁场时速度延长线必过圆心(如图 2)。利用这两个结论可以轻松画出带电粒子的运动轨迹,找出相应的几何关系。例 1.如图 3 所示,直线MN上方有磁感应强度为B的匀强磁场。正、负电子同时从同一点 O以与 MN成 30° 角的同样速度v 射入磁场(电子质量为m,电荷为e),它们从磁场中射出时相距多远?射出的时间差是多少?解析: 正、负电子的半径和周期是相同的。只是偏转方向相反。先确定圆心,画出半径和轨迹(如图4),由对称性知:射入、射出点和圆心恰好组成正三角形。所以两个射出点相距 s=2r =,由图还看出经历时间相差,所以解此题的关键是找圆心、找半径和用对称。例 2.如图 5 所示,在半径为r 的圆形区域内,有一个匀强磁场。一带电粒子以速度v0从 M点沿半径方向射入磁场区,并由N点射出, O点为圆心。当∠MON=120° 时,求:带电粒子在磁场区的偏转半径R及在磁场区中的运动时间。解析: 分别过 M、N点作半径OM、ON的垂线,此两垂线的交点O'即为带电粒子作圆周运动时圆弧轨道的圆心,如图6 所示。由图中的几何关系可知,圆弧MN所对的轨道圆心角为60° , O、O' 的边线为该圆心角的角平分线,由此可得带电粒子圆轨道半径为R=r/tan30 ° =又 带 电 粒 子 的 轨 道 半 径 可 表 示 为 :故 带 电 粒 子 运 动 周 期 :带电粒子在磁场区域中运动的时间二、旋转圆法在磁场中向垂直于磁场的各个方向发射速度大小相同的带电粒子时,带电粒子的运动轨迹是围绕发射点旋转的半径相同的动态圆(如图7),用这一规律可快速确定粒子的运动轨迹。例 3.如图 8 所示,S为电子源, 它在纸面 360° 度范围内发射速度大小为v0,质量为 m,电量为 q 的电子( q<0), MN是一块足够大的竖直挡板,与S 的水平距离为L,挡板左侧充满垂直纸面向外的匀强磁场,磁感应强度大小为mv0/ qL,求挡板被电子击中的范围为多大?解析: 由于粒子从同一点向各个方向发射,粒子的轨迹为绕S 点旋转的动态圆, 且动态圆的每一个圆都是逆时针旋转,这样可以作出打到最高点与最低点的轨迹,如图 9 所示, 最高点为动态圆与MN的相切...