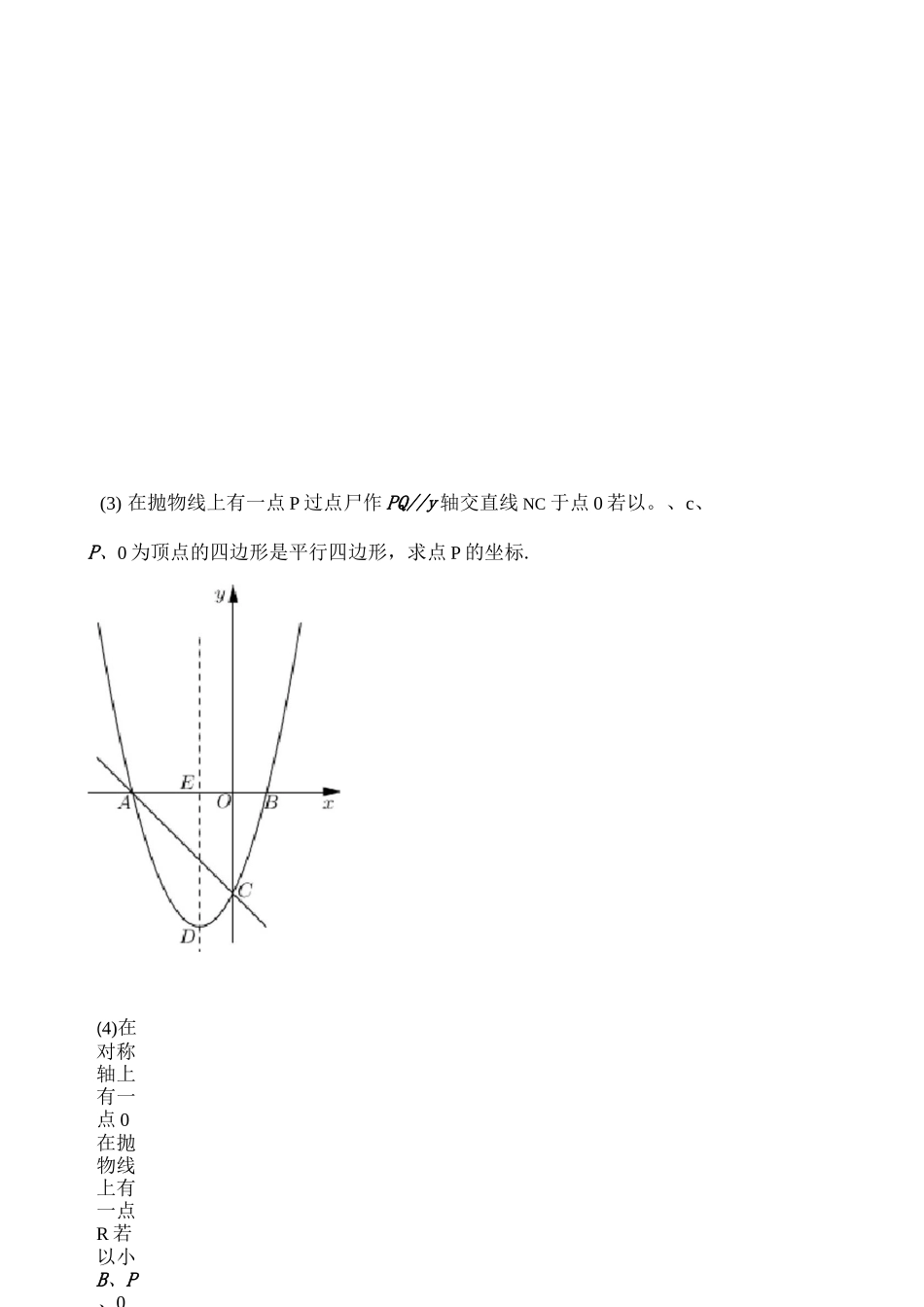
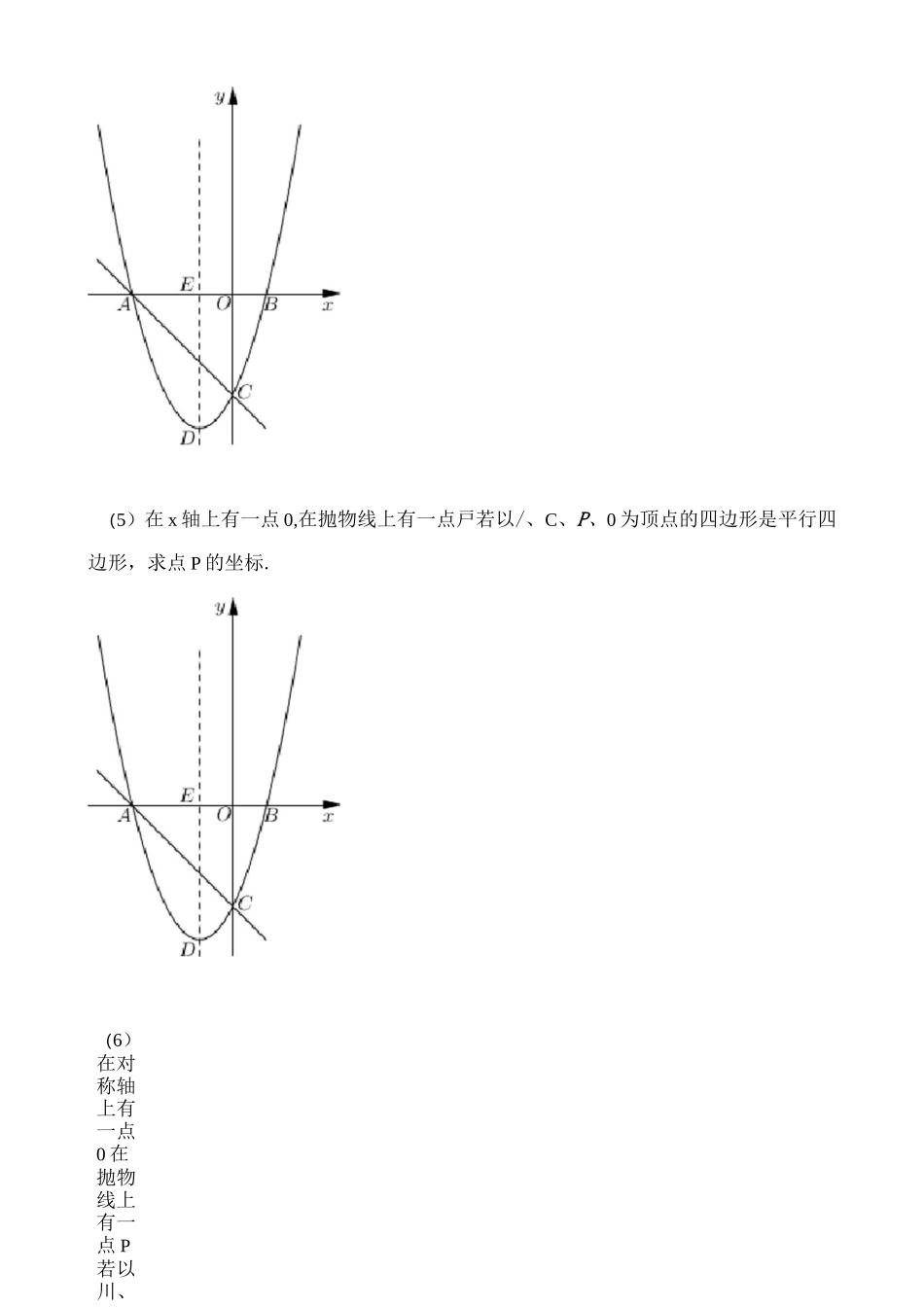
专题特殊四边形存在性问丿策略:①中点坐标公式;②三平三交定三点;③两对角线端点的横、纵坐标之和分别相等(秒杀必备);④横平竖直做辅助.三定一动:用②③即可秒杀(本质还分类两定点之间线段是一条边中点坐标公式)两 定 一 一 两 动 利 用 ① ② ③ ④ 综 合 解 决 两 定 点 之 间 线 段 一 条 对 角 线【母题】1.如图,在平面直角坐标系 xQy 中,抛物线 y=x2+bx+c 与 x 轴交于小 8 两点(点 2 在点 8 的左侧),与 y 轴交于点 C,OA=OC=3t顶点为 D,对称轴交 x 轴于点 E.(1)求抛物线的解析式、对称轴及顶点 D 的坐标.(2)在坐标平而内有一点 M 若以力、B、C、N 为顶点的四边形是平行四边形,求点 N的坐标•(4)在对称轴上有一点 0在抛物线上有一点R 若以小B、P、0(3) 在抛物线上有一点 P 过点尸作 PQ//y 轴交直线 NC 于点 0 若以。、c、P、0 为顶点的四边形是平行四边形,求点 P 的坐标.(6)在对称轴上有一点0 在抛物线上有一点 P若以川、C、P(4)在对称轴上有一点 0在抛物线上有一点R 若以小B、P、0(5)在 x 轴上有一点 0,在抛物线上有一点戸若以/、C、P、0 为顶点的四边形是平行四边形,求点 P 的坐标.(6)在对称轴上有一点0 在抛物线上有一点 P若以川、C、P(8)在对称轴上有一点0,在抛物线上有一点 P若以C、D、P(7)在对称轴上有一点 N,在平而内存在点若以厦、C、A/、N 为顶点的四边(8)在对称轴上有一点0,在抛物线上有一点 P若以C、D、P(9)在 y 轴上有一点在坐标平面内有一点 N,若以 2、C、AAN 为顶点的四边形是正方形,求点 N 的坐标.【答案】(1)y=x2+2x-3,对称轴为:直线 x=-l,顶点坐标为:D—(1,-4);(2)N 点坐标为:(-4,-3)或(一 2,3)或(2,-3);(3)P 点坐标为:-3+VH-3+VH-3-727-3-^/21⑷“点坐标为:(一 1,一 4)或(3,12)2222或(一 5,12);(5)P 点坐标为:(一 2,-3);或(―1+J7,3)或(-1-V7,3);(6)N 点坐标为:(-2,-3)或(2,5)或(一 4,5);(7)点皿坐标为(2,—0=(—3)'-3b+c—3=cb=2c=-3即:—3+0=1+心 0-3=0+〃有:—3+1=0+xN0+0=〃一 3心=-2儿=3有:—3+=0+11)或(一 4,-1)或(-2,二护 7)或(一 2,二半厅);(8)以 C、D、P、0为顶点的四边形是菱形,点 0的坐标为(一 1,-2);(9)点 N坐标为(一 3,-3)或(3,0)【解析】【分析】【详解】答案:(1)解:・・...