三角函数讲义

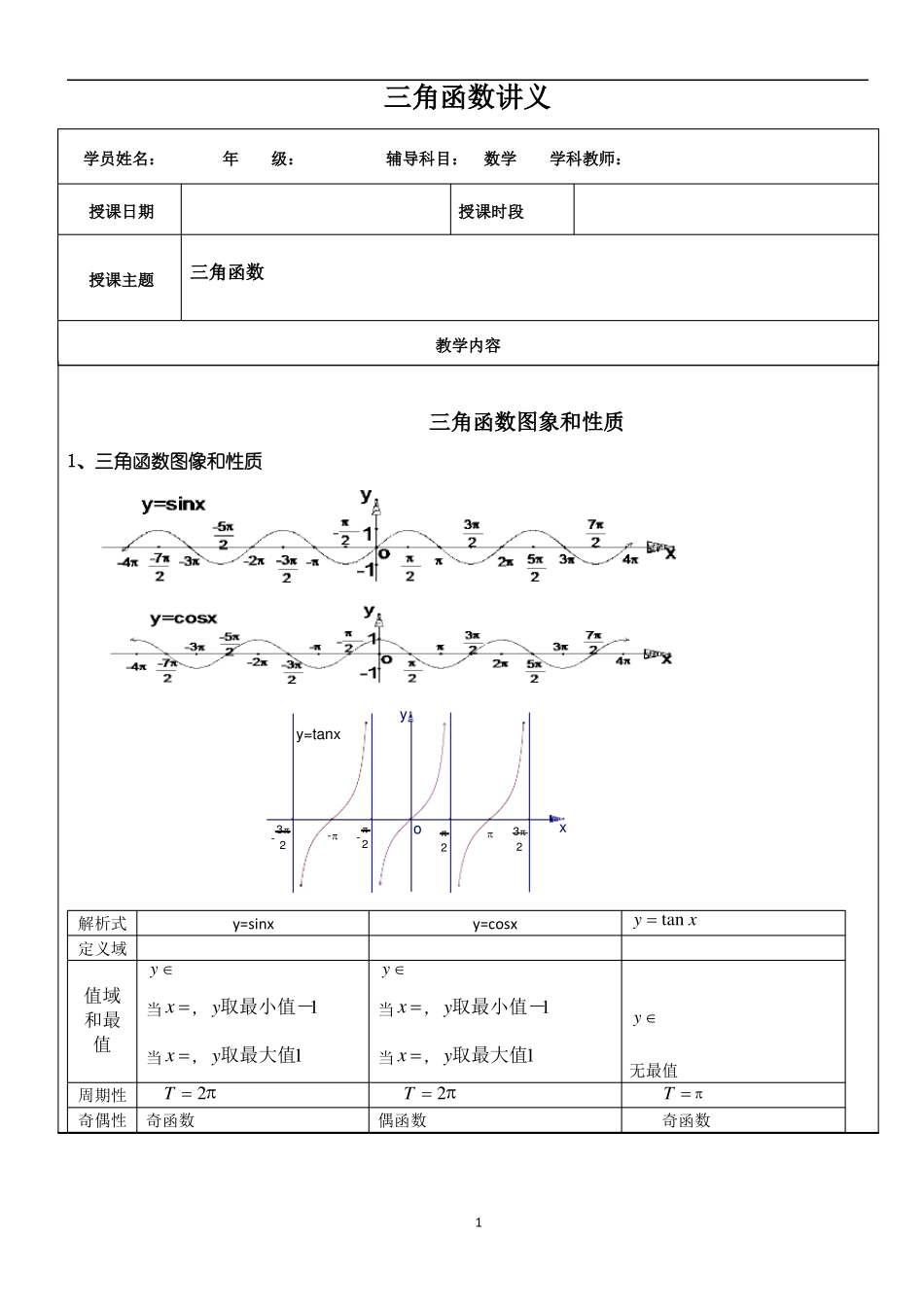
三角函数讲义学员姓名：年级：辅导科目：数学学科教师：授课日期授课时段授课主题三角函数教学内容三角函数图象和性质1、三角函数图像和性质yy=tanx- 32-- 2o232x解析式定义域y=sinxy=cosxy  tan xy y 值域和最值周期性1当 x ， y取最小值－当 x ， y取最大值11当 x ， y取最小值－当 x ， y取最大值1y 无最值T  2T  2偶函数T  奇函数奇偶性奇函数1k Z在 2k   ，2k  22单调性上是增函数 k Z在 2k   ，2k  322在 2k ，2k k Z 上 是 增函数在 k 2 ,k    k Z2 在 2k，2k  k Z 上 是 减函数对称中心(k上为增函数上是减函数对称中心(k,0)k  Z对称性对 称 轴 方 程 2 ,0) k Z对称中心(k,0)k  Z或者对称中心(kx  k  2 ，对称轴方程 x  k ，k Zk Z 2 ,0) k Z2、熟练求函数 y  Asin(x ) 的值域，最值，周期，单调区间，对称轴、对称中心等，会用五点法作 y  Asin(x ) 简图：五点分别为：、、、、。3、图象的基本变换：相位变换： y  sin x  y  sin(x  )周期变换： y  sin(x )  y  sin(x )振幅变换： y  sin(x )  y  Asin(x )4、求函数 y  Asin(x ) 的解析式：即求 A 由最值确定，ω 有周期确定，φ 有特殊点确定。5、三角函数最值类型：（1）y=asinx+bcosx 型函数最值的求法：常转化为 y=a2 b2 sin（x+ ）（2）y=asin2x+bsinx+c 型：常通过换元法（令 sinx=t，t 1,1）转化为 y=at2+bt+c 型：（3）同一问题中出现sin x  cos x,sin x  cos x,sin x  cos x ，求它们的范围时，一般是令 sin x  cos x  tt 2 1t 2 1或sin x  cos x  t  sin xcos x 或sin x cos x  ，转化为关于t 的二次函数来解决22三、三角形知识：（1） ABC 中， a,b,c 分别为 A, B,C 的对边， A  B  C  a  b  c  sin A  sin B  sin C 。（2）在 ABC 中，A+B+C=180°2三角函数题型分类总结一．求值4 ,tan  0 ，则cos  .515...