六年级上册数学奥数-速算与巧算档含答案

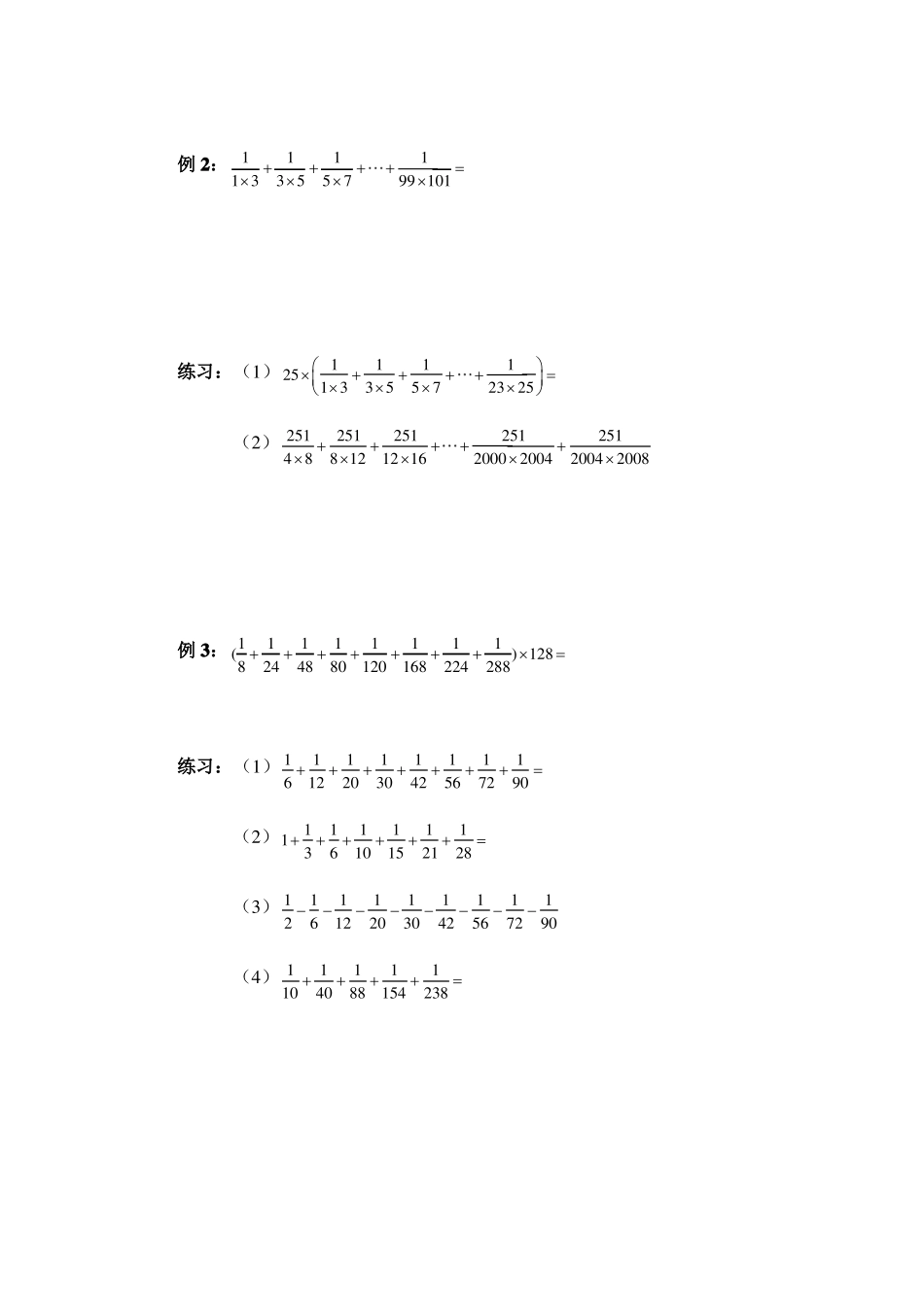
六年级下册奥数 速算与巧算（裂项法）1、分数裂项法将算式中的项进行拆分，使拆分后的项可前后抵消，这种拆项计算称为裂项法。裂项分为分数裂项和整数裂项，常见的裂项方法是将数字分拆成两个或多个数字单位的和或差。遇到裂项的计算题时，要仔细的观察每项的分子和分母，找出每项分子分母之间具有的相同的关系，找出共有部分，裂项的题目无需复杂的计算，一般都是中间部分消去的过程，这样的话，找到相邻两项的相似部分，让它们消去才是最根本的。1(1)对于分母可以写作两个因数乘积的分数，即 ab 形式的，这里我们把较1111()a  ba bb  a ab小的数写在前面，即，那么有(2)对于分母上为 3 个或 4 个连续自然数乘积形式的分数，即：11n (n 1)(n  2) ， n(n 1)(n  2)(n  3) 形式的，我们有：1111[]n (n 1) (n  2)2 n(n 1)(n 1)(n  2)1111[]n (n 1) (n  2)(n  3)3 n(n 1)(n  2)(n 1)(n  2)(n  3)裂差型裂项的三大关键特征：（1）分子全部相同，最简单形式为都是 1 的，复杂形式可为都是 x(x 为任意自然数)的，但是只要将 x 提取出来即可转化为分子都是 1 的运算。（2）分母上均为几个自然数的乘积形式，并且满足相邻 2 个分母上的因数“首尾相接”（3）分母上几个因数间的差是一个定值。2、整数裂项法：裂项思想是：瞻前顾后，相互抵消。例如：1 2  2 3 3 4 设 S＝1 2  2 3 3 4  49 50 =_________； 4950 1×2×3＝1×2×32×3×3＝2×3×（4－1）＝2×3×4－1×2×33×4×3＝3×4×（5－2）＝3×4×5－2×3×4……49×50×3＝49×50×（51－48）=49×50×51－48×49×503S＝1×2×3＋2×3×3＋3×4×3＋…＋49×50×3＝49×50×51 S＝49×50×51÷3＝41650例 1：11111。1 2233 44556练习：（1）111......1011111259602210998225 443（2）例 2：练习：（1） 2511113355 71 23 25 111133557199101（2） 2512512514881212162512512000 20042004 2008例 3： ( 181111111)128 244880120168224288练习：（1）111111116122030425672901316111110152128...