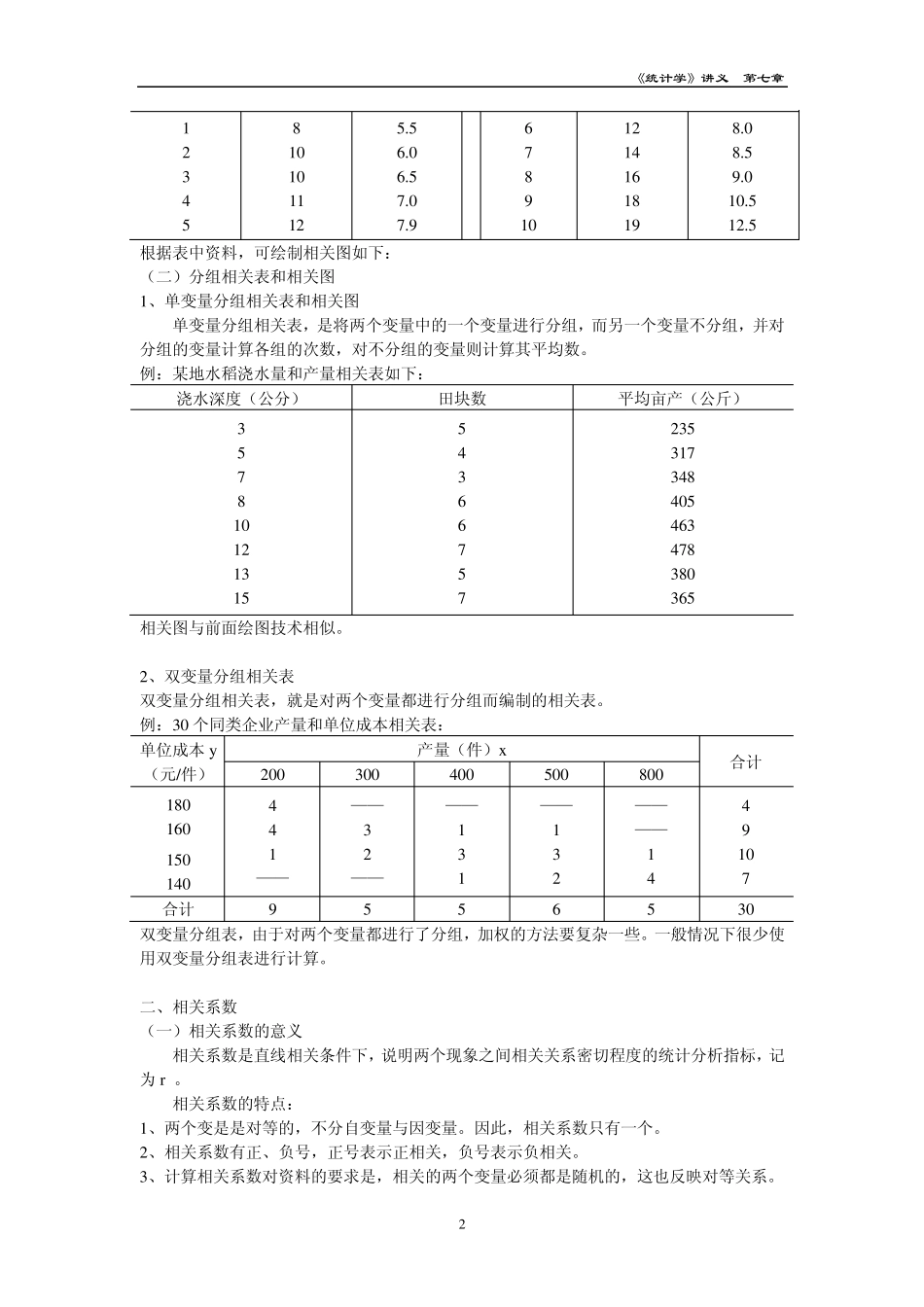
《统计学》讲义 第七章 1 第七章 相关与回归分析 第一节 相关分析的意义和种类 一、相关分析的概念 现象之间的相互关系可以分为两种不同的类型: (一)函数关系 它反映现象之间存在着严格的依存关系,在这种关系中,对于某一个变量的每一个数值,都有另一个变量的确定值与之相对应,并且这种关系可用一个函数式表达出来。例如:圆周长 L 与圆半径 r 之间存在严格的确定性关系,因而两者的相关关系为函数关系,即rL2。 (二)相关关系 它反映现象之间客观存在的、不严格、不确的相互依存关系。这种关系不能通个别现象体现其关系的规律性,必须在大量现象中才能体现出来。 相关分析是研究一个变量(y)与另一个变量(x )之间相关方向与相关密切程度的一种统计分析方法。 二、相关关系的种类 (一) 按相关的方向分为正相关和负相关 正相关是指两个变量之间的变化方向一致,都是增长趋势或下降趋势。 负相关是指两个变量之间的变化趋势方向相反,一个上升而另一个下降。 (二)按相关的形式可分为直线相关的非直线相关 直线相关,又称线性相关。是指当相关关系的一个变量变动时,另一个变量也相应地发生大致均等的变动。 非直线相关,又称非线性相关或曲线相关。是指当相关关系的一个变量变动时,另一个蛮量也相应地发生变动,但这种变动是不均等的。 正、负相关散点图及曲线相关散点图下如: 三、相关分析的主要内容 1、确定现象之间有无关系存在,以及相关关系的形态。 2、确定相关关系的密切程度。 3、确定相关关系的数学表达式。如果现象之间的关系是直线相关,则配合线性方程;如果是曲线相关,则配合曲线方程。这是进行判断、推算和预测的依据。 4、确定因变量估计值误差程度。确定因变量估计值误差大小的指标是估计标准误差,估计标准误差大,表明估计不太精确;估计标准误差大小,表明估计较精确。 第二节 相关关系的测定 一、相关表和相关图 (一)简单相关表和相关图 对资料较少的,可不分组,只将自变的变量值值按大小顺序加以排列,因变量的变量值一一加以对应,排列其变量值则可编成简单相关表。 例:某企业工人劳动生产率和利润率相关表如下: 序号 工人劳动生产率(千元) 利润率(%) 序号 工人劳动生产率(千元) 利润率(%) 《统计学》讲义 第七章 2 1 2 3 4 5 8 10 10 11 12 5.5 6.0 6.5 7.0 7.9 6 7 8 9 10 12 14 16 18 19 8.0 8.5 9.0 10.5 ...