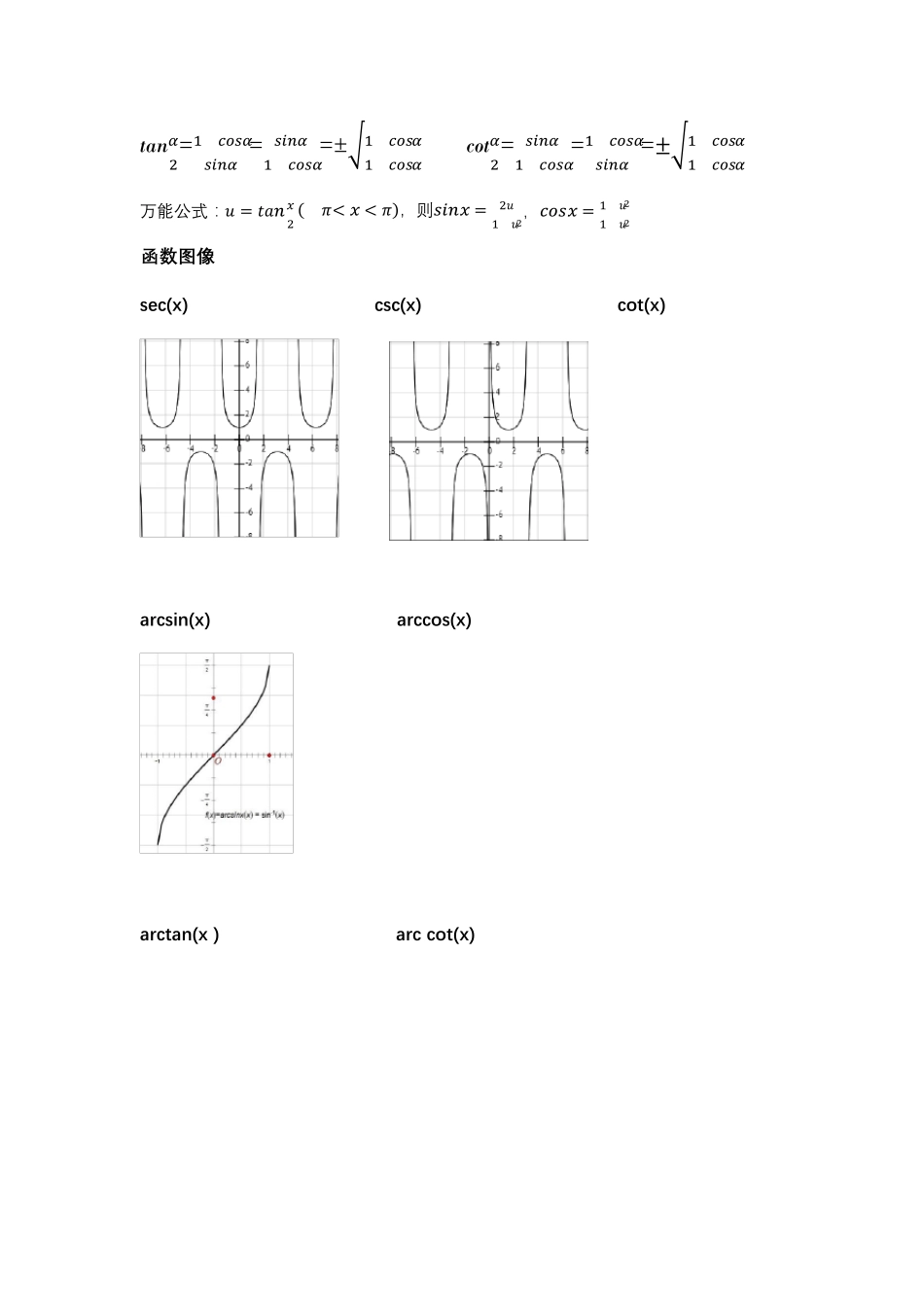
[基础知识] 因式分解公式:ᵄᵅ-ᵄᵅ=(ᵄ-b)( ᵄᵅ−1+ᵄᵅ−2b+…+ᵄᵄᵅ−2+ᵄᵅ−1) ( n 为 正 偶 数 时 )ᵄᵅ-ᵄᵅ=(ᵄ+b)( ᵄᵅ−1-ᵄᵅ−2b+…+ᵄᵄᵅ−2-ᵄᵅ−1) ( n 为 正 奇 数 时 )ᵄᵅ+ᵄᵅ=(ᵄ+b)( ᵄᵅ−1-ᵄᵅ−2b+…-ᵄᵄᵅ−2+ᵄᵅ−1) 二项式定理:(ᵄ + ᵄ)ᵅ=∑ᵃᵅᵅᵄᵅᵄᵅ−ᵅᵅᵅ=0 不等式: (1) a,b 位实数,则 ○1 ᵽ|ab| ≤ ᵄ2 + ᵄ2; ○2 |ᵄ ± ᵄ| ≤ |ᵄ| + |ᵄ|; ○3 |ᵄ| −|ᵄ|≤ |ᵄ −ᵄ|. (2) ᵁᵼ, ᵁᵽ,…,ᵁᵂ>0, 则 ○1 ᵄ1+ᵄ2+⋯+ᵄᵅᵅ≥ √ᵄ1ᵄ2 ⋯ ᵄᵅᵅ 取 整 函 数:x-1< [x]≤x 三 角 函 数 和 差 化 积 ;积 化 和 差 (7): sinα+sinβ=2(sinᵯ+ᵯ2)(cosᵯ−ᵯ2) sinαcosβ=12(sinᵯ+ᵯ2+cosᵯ−ᵯ2) sinα-sinβ=2(cosᵯ+ᵯ2)(sinᵯ−ᵯ2) cosαcosβ=12(cosᵯ+ᵯ2+cosᵯ−ᵯ2) cosα+cosβ=2(cosᵯ+ᵯ2)(coᵆ ᵯ−ᵯ2) sinαsinβ=-12(cosᵯ+ᵯ2-cosᵯ−ᵯ2) cosα-cosβ=2(sinᵯ+ᵯ2)(sinᵯ−ᵯ2) 重 要 三 角 公式 1+ᵆᵄᵅ2 ᵯ=ᵆᵅᵅ2 ᵯ 1+ᵅᵅᵆ2 ᵯ=ᵅᵆᵅ2 ᵯ ᵆᵅᵅ2ᵯ =2ᵆᵅᵅᵯᵅᵅᵆ ᵯ ᵅᵅᵆ 2ᵯ=ᵅᵅᵆ2 ᵯ-ᵆᵅᵅ2 ᵯ=1-2ᵆᵅᵅ2 ᵯ=2ᵅᵅᵆ2 ᵯ-1 tan(ᵯ ± ᵯ)= ᵆᵄᵅᵯ±ᵆᵄᵅᵯ1∓ ᵆᵄᵅᵯ tan ᵯ cot(ᵯ ± ᵯ) =1∓ cot ᵯ cot ᵯcot ᵯ+cot ᵯ tanᵯ2=1−ᵅᵅᵆᵯᵆᵅᵅᵯ= ᵆᵅᵅᵯ1+ᵅᵅᵆᵯ=± √1−ᵅᵅᵆᵯ1+ᵅᵅᵆᵯ cotᵯ2= ᵆᵅᵅᵯ1−ᵅᵅᵆᵯ=1+ᵅᵅᵆᵯᵆᵅᵅᵯ=±√1+ᵅᵅᵆᵯ1−ᵅᵅᵆᵯ 万 能 公 式 : ᵆ = ᵆᵄᵅᵆ2 (−ᵰ< ᵆ < ᵰ), 则 ᵆᵅᵅᵆ =2ᵆ1+ᵆ2, ᵅᵅᵆᵆ = 1−ᵆ21+ᵆ2 函 数 图 像 sec(x) csc(x) cot(x) arcsin(x) arccos(x) arctan(x ) arc cot(x) [极限] 定义 函数极限 x→• :( 6) ᵅᵅᵅᵆ→ᵆ0 ᵅ(ᵆ)=A: ∀ᵍ>0,∃ᵬ>0,当0<|x- x0|< ᵬ时 , 恒 有 |f(x)-A|< ᵍ. ᵅᵅᵅᵆ→ᵆ0+ᵅ(ᵆ)=A: ∀ᵍ>0,∃ᵬ>0,当0<(x- x0)< ᵬ时 , 恒 有 |f(x)-A|< ᵍ. ᵅᵅᵅᵆ→ᵆ0−ᵅ(ᵆ)=A: ∀ᵍ>0,∃ᵬ>0,当0<( x0- x)< ᵬ时 , 恒 有 |f(x)-A|< ᵍ. ᵅᵅᵅᵆ→∞ ᵅ(ᵆ)=A: ∀ᵍ>0, ∃X>0,当 |x|>X 时 ,恒 有 |f(x)-A|< ᵍ. ᵅᵅᵅᵆ→∞+ ᵅ(ᵆ)=A: ∀ᵍ>0, ∃X>0,当x>X 时 ,恒 有 |f(x)-A|< ᵍ. ...