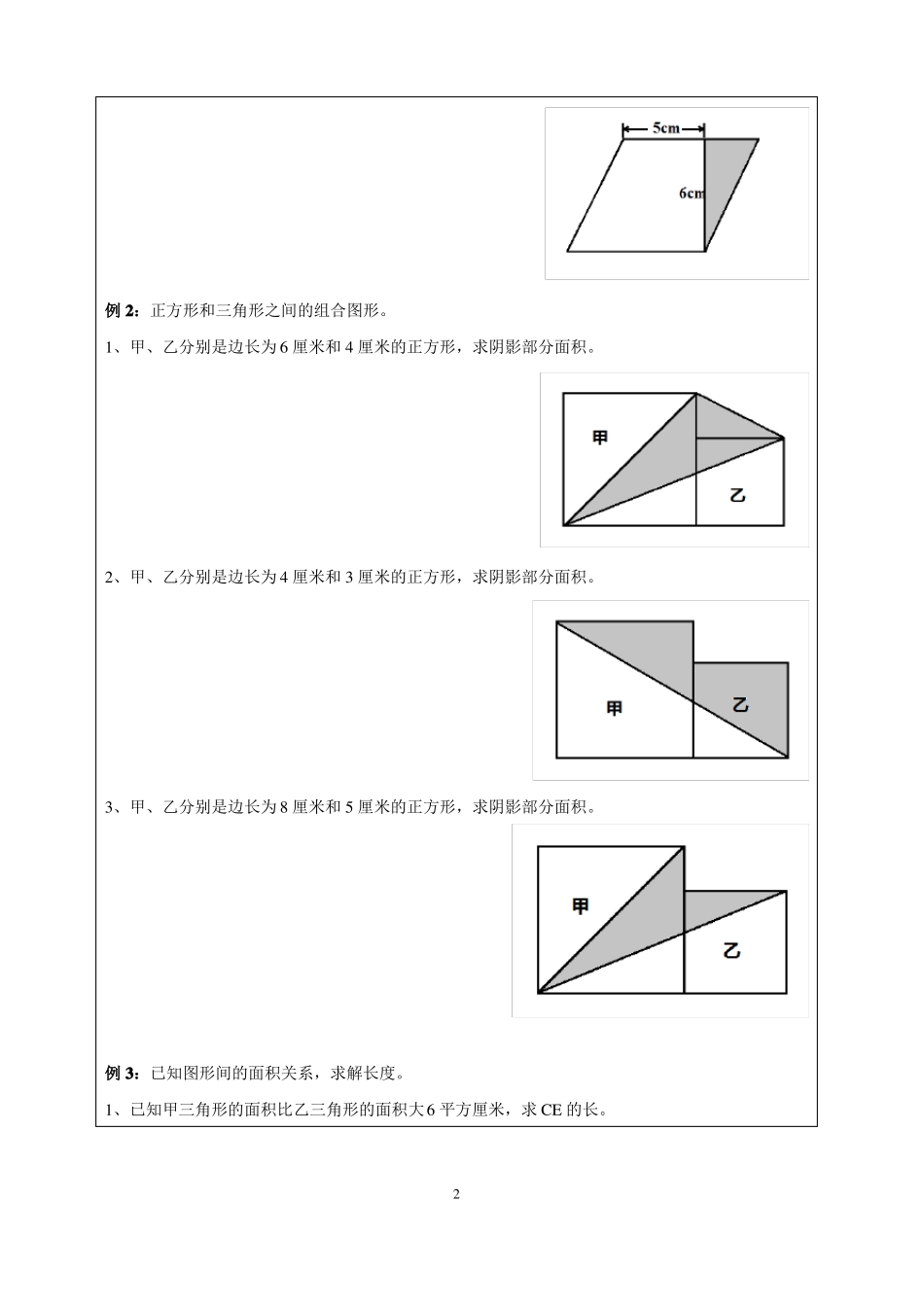
辅导讲义教学内容一、能力培养几何图形是数学里非常重要的知识,它主要包括长度、面积、体积等方面,也是升学、分班考试必考的内容(比较侧重于阴影部分的面积)。今天我们重点来研究这一板块的计算问题。我们已经掌握了几种基本图形的面积计算方法,我们先来复习一下。正方形面积=边长×边长=对角线 2÷2长方形面积=长×宽平行四边形面积=底×高三角形面积=底×高÷2梯形面积=(上底+下底)×高÷2圆面积=半径 2×π。由两个甚至更多的基本图形组合在一起,就构成了一个组合图形。要计算组合图形的面积,就要根据图形的关系,灵活运用平移、旋转、分割、拼接、等积变形等方法。下面我们来看看具体的题目。如果你都会做,你就无敌了。例 1:基本图形的面积计算。1、下图的梯形中,阴影部分的面积是 150 平方厘米,求梯形的面积。2、已知平行四边形的面积是 48 平方厘米,求阴影部分的面积。1例 2:正方形和三角形之间的组合图形。1、甲、乙分别是边长为 6 厘米和 4 厘米的正方形,求阴影部分面积。2、甲、乙分别是边长为 4 厘米和 3 厘米的正方形,求阴影部分面积。3、甲、乙分别是边长为 8 厘米和 5 厘米的正方形,求阴影部分面积。例 3:已知图形间的面积关系,求解长度。1、已知甲三角形的面积比乙三角形的面积大6 平方厘米,求 CE 的长。22、四边形 ABCD 是长为 10 厘米,宽 6 厘米的长方形,三角形 ADE 的面积比三角形 CEF 的面积大10 平方厘米。求 CF 的长。3、平行四边形 ABCD 中,BC=10 厘米。直角三角形 BCE 的直角边 EC=8 厘米。已知阴影部分的面积比三角形 EFG 的面积大 10 平方厘米。求 CF 的长。例 4:等积变形。1、已知小正方形的边长是 4 厘米,求阴影部分的面积。32、已知大正方形的边长是 6 分米,求阴影部分的面积。3、三角形 ABC 的面积是 30 平方厘米,D 是 BC 中点,AE 的长度是 ED 的 2 倍,求阴影部分的面积。4、已知中间小三角形的面积是5 平方厘米,把三角形的三条边都向外延长,使得延长线段的长度与原来小三角形的对应边长都相等,求大三角形 ABC 的面积。45、如图,长方形 ABCD,三角形 ABG 的面积是 20,三角形 CDQ 的面积是 35,求阴影部分面积。6、在梯形 ABCD 中,对角线 AC、BD 相交于 O,已知 AO:CO=1:2,S△AOD=30,求梯形 ABCD 的面积。例 5:用“排空法、平移旋转法、二次求差法”解决有关圆的组合图形。1、求阴影部...