一元二次方程复习专题讲义(补课用)

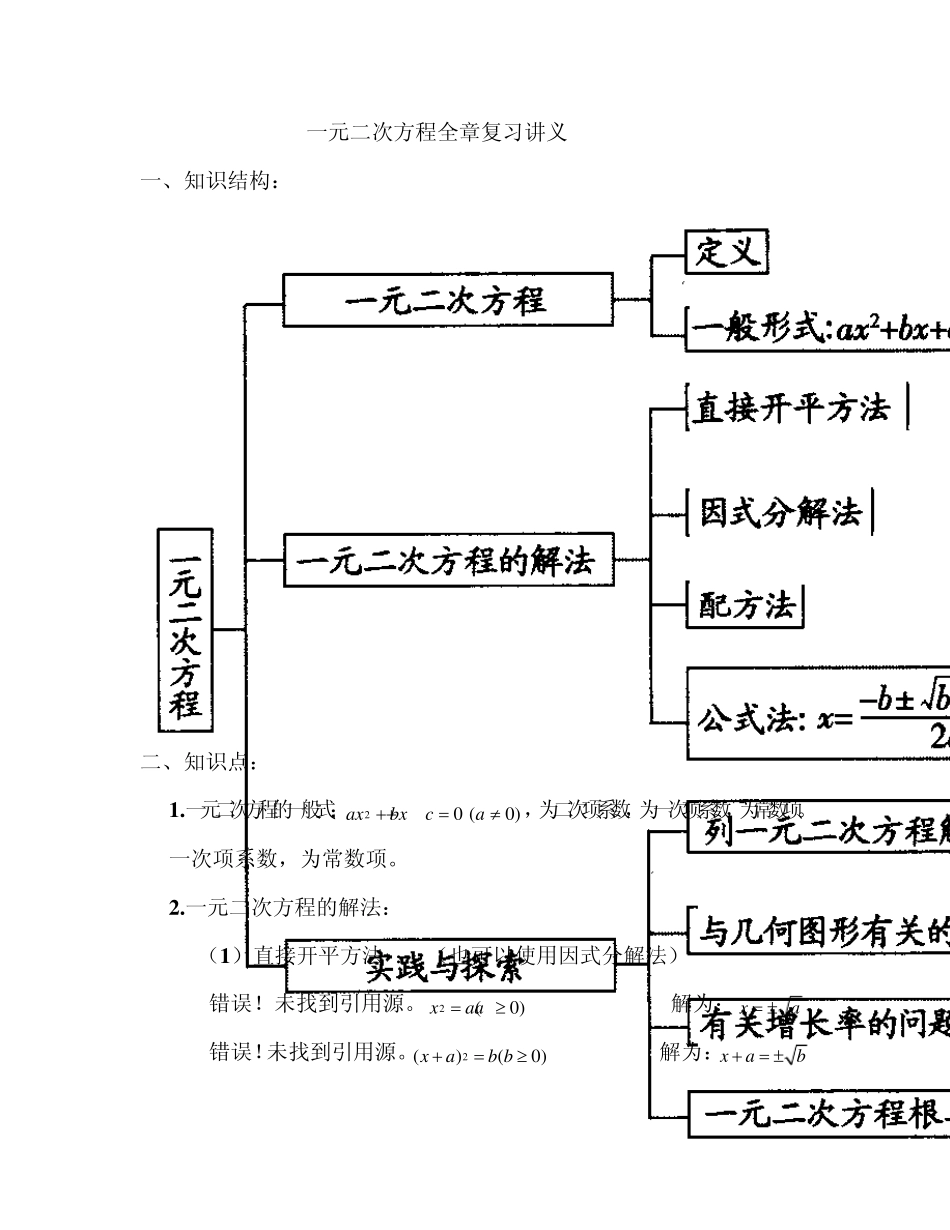
一元二次方程全章复习讲义 一、知识结构： 二、知识点： 1 .一元二次方程的一般式：20 (0 )axbxca，为二次项系数，为一次项系数，为常数项。 一次项系数，为常数项。 2 .一元二次方程的解法： （1 ）直接开平方法 ： （也可以使用因式分解法） 错误！未找到引用源。2(0 )xaa 解为： xa  错误！未找到引用源。2()(0 )xab b 解为：xab  错误！未找到引用源。2()(0 )axbc c 解为：axbc  错误！未找到引用源。22()() ()axbcxdac 解为：()axbcxd  （2）因式分解法：提公因式分解，平方公式，平方差，十字相乘法。如：20 ( ,0 )()0axbxabx axb 此类方程适合用提公因式，而且其中一个根为0。 290(3 )(3 )0xxx   23 0(3 )0xxx x  3 (21 )5 (21 )0(35 )(21 )0xxxxx    22694 (3 )4xxx 224 1290(23 )0xxx x2-4x-12=0(x-6)(x+2)=0 2x2+5x-12=0(2x-3)(x+4)=0 (3) 配方法： 错误！未找到引用源。二次项的系数为“1”的时候：直接将一次项的系数除于 2 进行配方，如下所示： 2220()()022PPxPxqxq 示例：22233310 ()( )1022xxx   错误！未找到引用源。二次项的系数不为“1”的时候：先提取二次项的系数，之后的方法同上： 22220 (0 )()0 ()()022bbbaxbxcaa xxca xacaaa 222224()()2424bbbbaca xcxaaaa 示例： 22221111210(4) 10(2 )2102222xxxxx    (4 ).公式法： 一元二次方程20 (0 )axbxca，用配方法将其变形为： 2224()24bbacxaa 错误！未找到引用源。当240bac  时，右端是正数．因此，方程有两个不相等的实根：21 ,242bbacxa  错误！未找到引用源。 当240bac  时，右端是零．因此，方程有两个相等的实根：1 ,22bxa  错误！未找到引用源。 当240bac  时，右端是负数．因此，方程没有实根。 3 .公式法解方程的步骤： 错误！未找到引用源。把方程化成一般形式： 一元二次方程的一般式：20 (0 )axbxca，并确定出、、 错误！未找到引用源。求出24bac ，并判断方程解的情况。 I当△>0时，一元二次方程有2个不相等的...