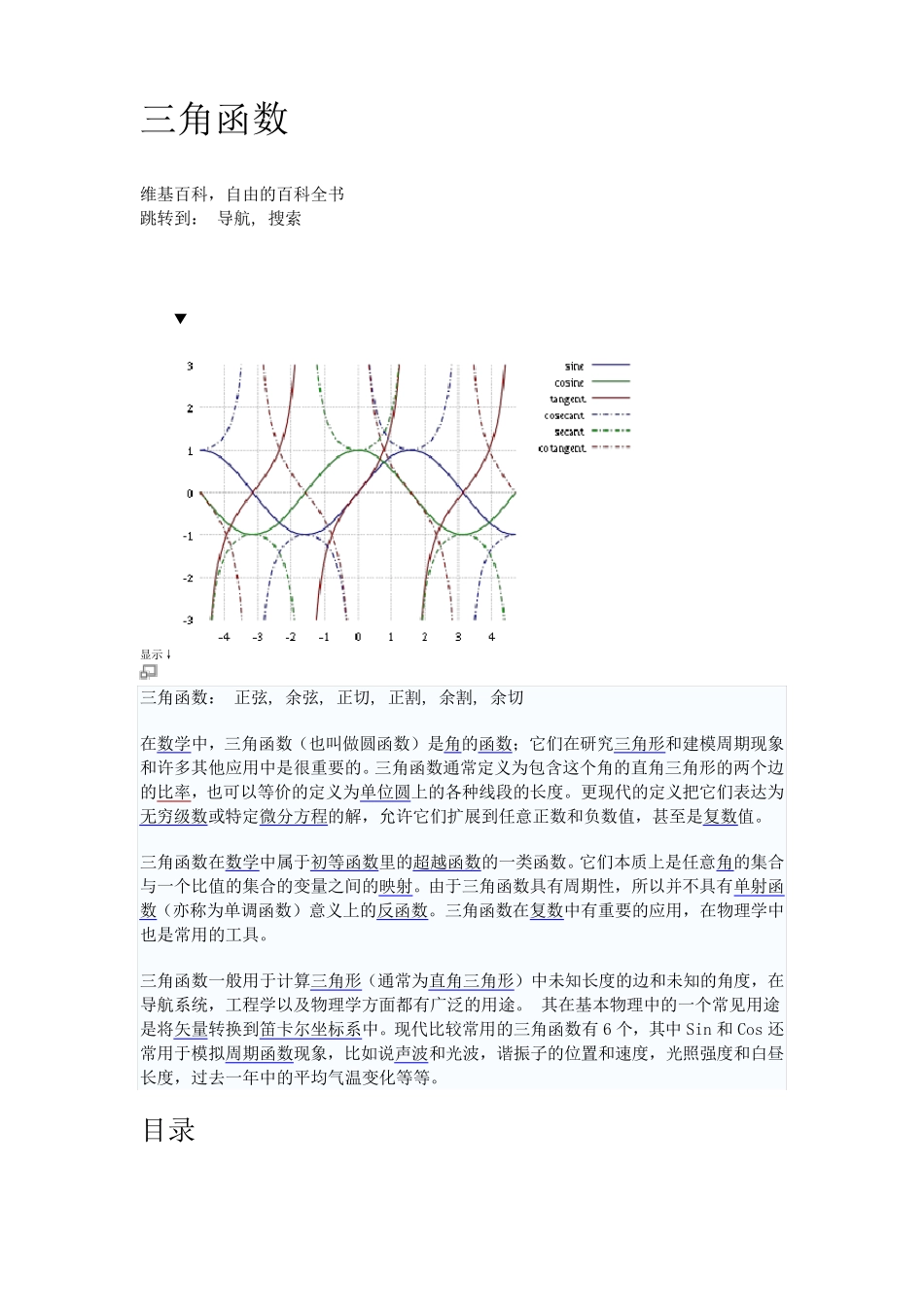
三角函数 维基百科,自由的百科全书 跳转到: 导航, 搜索 ▼ 显示↓ 三角函数: 正弦, 余弦, 正切, 正割, 余割, 余切 在数学中,三角函数(也叫做圆函数)是角的函数;它们在研究三角形和建模周期现象和许多其他应用中是很重要的。三角函数通常定义为包含这个角的直角三角形的两个边的比率,也可以等价的定义为单位圆上的各种线段的长度。更现代的定义把它们表达为无穷级数或特定微分方程的解,允许它们扩展到任意正数和负数值,甚至是复数值。 三角函数在数学中属于初等函数里的超越函数的一类函数。它们本质上是任意角的集合与一个比值的集合的变量之间的映射。由于三角函数具有周期性,所以并不具有单射函数(亦称为单调函数)意义上的反函数。三角函数在复数中有重要的应用,在物理学中也是常用的工具。 三角函数一般用于计算三角形(通常为直角三角形)中未知长度的边和未知的角度,在导航系统,工程学以及物理学方面都有广泛的用途 。 其在基本物理中的一个常见 用途是将 矢 量转换 到笛 卡 尔 坐 标 系中。现代比较 常用的三角函数有6 个,其中 Sin 和 Cos 还常用于模拟 周期函数现象,比如 说 声 波 和光 波 ,谐 振 子 的位置 和速 度,光 照 强 度和白 昼长度,过 去 一年 中的平 均 气 温 变化 等等。 目 录 [隐藏] • 1 基本函数 • 2 罕见函数 • 3 历史 • 4 直角三角定义 o 4.1 直角三角形中 o 4.2 直角坐标系中 • 5 单位圆定义 • 6 级数定义 o 6.1 与指数函数和复数的联系 • 7 微分方程定义 o 7.1 弧度的重要性 • 8 恒等式 o 8.1 微积分 o 8.2 利用函数方程定义三角函数 • 9 计算 o 9.1 三角函数的特殊值 • 10 反三角函数 • 11 性质和应用 o 11.1 正弦定理 o 11.2 余弦定理 o 11.3 正切定理 o 11.4 周期函数 • 12 注释 • 13 参考文献 • 14 参见 • 15 外部链接 [编辑] 基本函数 直角三角形。 如右图,当平面上的三点A、B、C 的连线,、、,构成一个直角三角形,其中为直角。对于与的夹角而言: 对边(opposite) 邻边(adjacent) 斜边(hypotenuse) 函数 英语 简写 定义 关系 正弦 Sine sin 余弦 Cosine cos 正切 Tangent tan 余切Cotangent cot 正割Secant sec 余割Cosecant csc 注:中国大陆早期教科书中多将正切、余切写作 tg,ctg,...