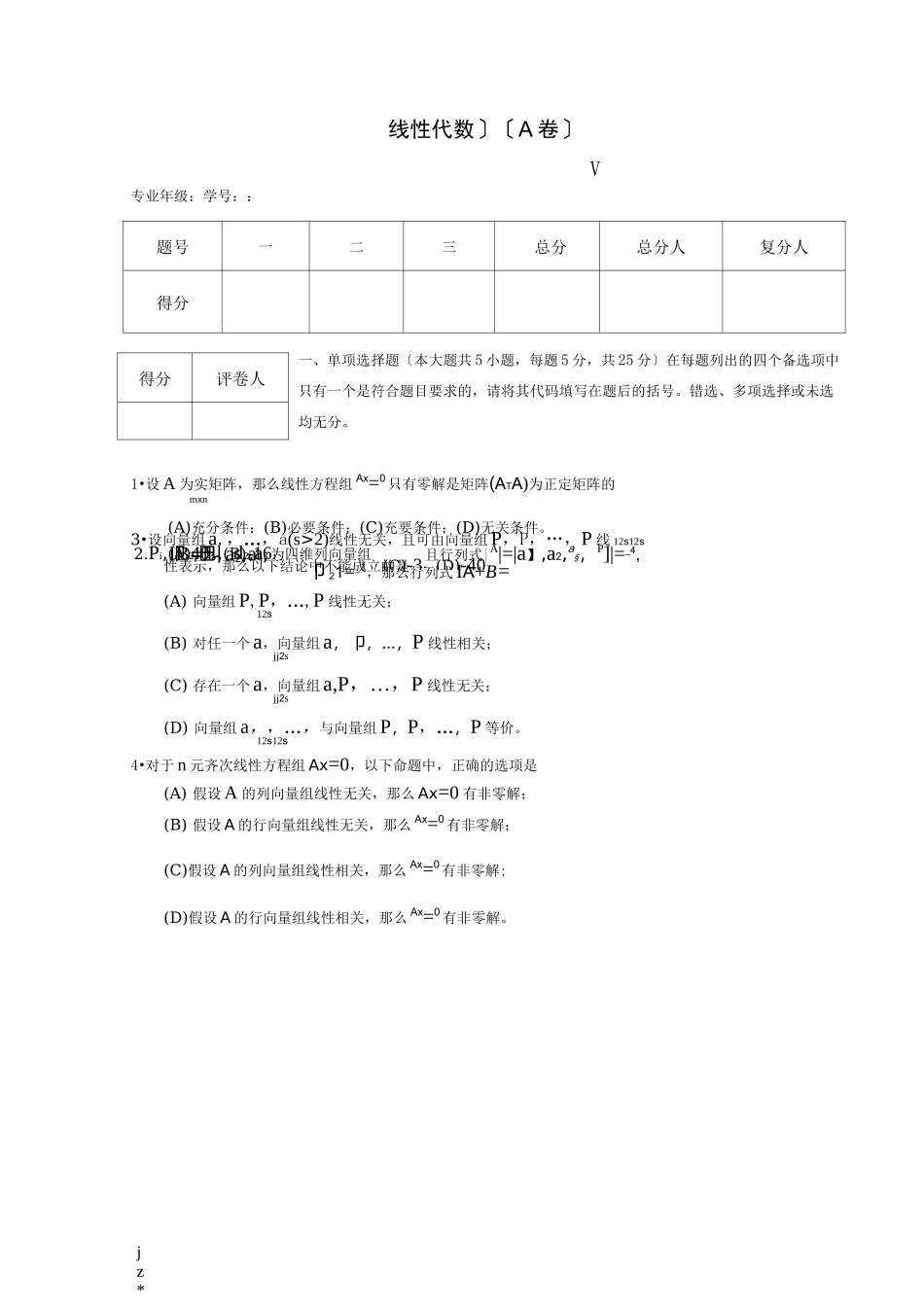
jz*2.Pi,卩 2,巴,d2,a3为四维列向量组且行列式|A|=|a】,a2,a§,P]|=_4,IB=叫 a2,a3,卩 21=_1,那么行列式IA+B=(A)40;(B)-16;(C)-3;(D)-40线性代数〕〔A 卷〕V专业年级:学号::题号一二三总分总分人复分人得分一、单项选择题〔本大题共 5 小题,每题 5 分,共 25 分〕在每题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号。错选、多项选择或未选均无分。1•设 A 为实矩阵,那么线性方程组 Ax=0只有零解是矩阵(ATA)为正定矩阵的mxn(A)充分条件;(B)必要条件;(C)充要条件;(D)无关条件。3•设向量组a,,…,a(s>2)线性无关,且可由向量组P,P,…,P 线 12s12s性表示,那么以下结论中不能成立的是(A) 向量组P,P,…,P 线性无关;12s(B) 对任一个a,向量组a,卩,…,P 线性相关;jj2s(C) 存在一个a,向量组a,P,…,P 线性无关;jj2s(D) 向量组a,,…,与向量组P,P,…,P 等价。12s12s4•对于 n 元齐次线性方程组 Ax=0,以下命题中,正确的选项是(A) 假设 A 的列向量组线性无关,那么 Ax=0 有非零解;(B) 假设 A 的行向量组线性无关,那么 Ax=0有非零解;(C)假设 A 的列向量组线性相关,那么 Ax=0有非零解;(D)假设 A 的行向量组线性相关,那么 Ax=0有非零解。得分评卷人jz*列向量a厂2是矩阵 A=5〔-5•设 A 为 n阶非奇异矩阵(n>2),A*为 A 的伴随矩阵,那么(A)(AT)*=1AI-iA;(B)(A-i)*=1AIA;(C)(A-I)*=IAI-iA-i;(D)(A-I)*=IAIA-1。二、填空题〔本大题共 5 小题,每题 5 分,共 25 分〕请在每题的空格中填上正确答案。错填、不填均无分。-12'a3 的对应特征值九的一个特征向量.b-2 丿那么九=,a=,b=。7. 设 n阶向量a=(x,,…,0,)T,x<0;矩阵 A=E-aaT,1且 A-i=E+—aaT,那么 x=。x8. 实二次型 f(xx,x)=x2+4x2+2x2+2axx+2xx 正定那么常数 a 的1,231231223取值围为。9•设矩阵 A=(ai),j3x3A 是 IAI 中元素 a 的代数余子式,a=Aijijijija=2a= 3a,a>0, 那么 a=。1112131111(1 2-2、(a110.设 A= 2 12a=1 ,向量 Aa与 a线性相关,那么 a=o<304‘J‘242x2一 5-1-23611.(1)求方程 f(x)=0的根,其中 f(x)=-32-1x2+3-21-2得分评卷人得分评卷人三、分析计算题(本大题共 5 小题,每题 10 分共 50分)jz*xx•…xy+x12n-1nxx•…y+xx12n-1n⑵ 计算 n阶行列式 D=…・・•••・・ ・・・・•xy+x•…xx12n-1ny+xx•…xx12n-1n12...