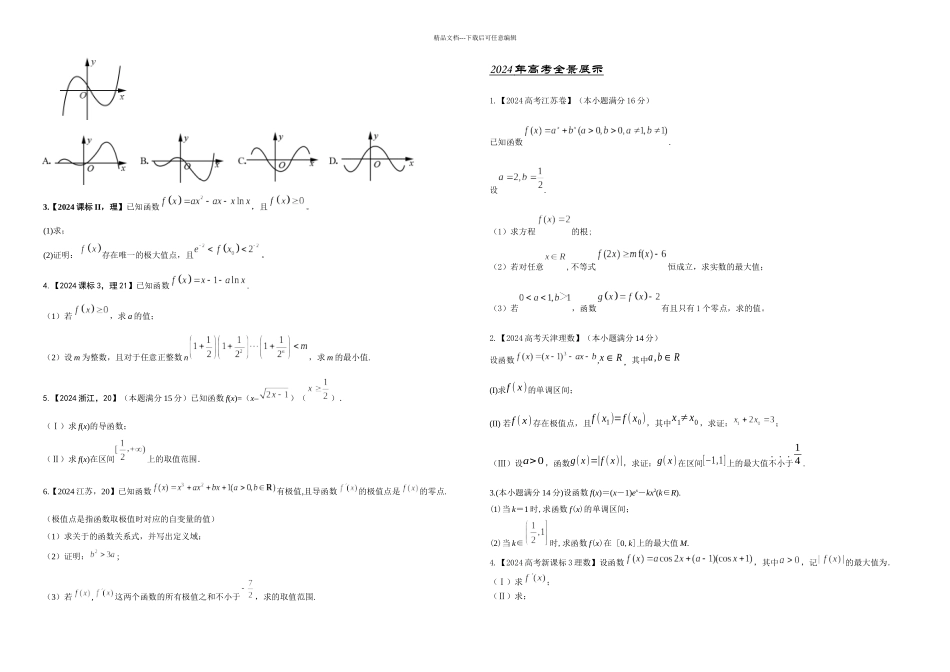
精品文档---下载后可任意编辑专题 07 导数的应用考纲解读明方向考点内容解读要求常考题型预测热度1.导数与函数的单调性了解函数单调性和导数的关系;能利用导数讨论函数的单调性,会求函数的单调区间(其中多项式函数一般不超过三次)理解选择题解答题★★★2.导数与函数的极(最)值了解函数在某点取得极值的必要条件和充分条件;会用导数求函数的极大值、微小值(其中多项式函数一般不超过三次);会求闭区间上函数的最大值、最小值(其中多项式函数一般不超过三次)掌握解答题★★★3.生活中的优化问题会利用导数解决某些实际问题掌握选择题★☆☆分析解读 1.会利用导数讨论函数的单调性,掌握求函数单调区间的方法.2.掌握求函数极值与最值的方法,解决利润最大、用料最省、效率最高等实际生产、生活中的优化问题.3.利用导数求函数极值与最值、结合单调性与最值求参数范围、证明不等式是高考热点.分值为 12~17 分,属于高档题.命题探究练扩展2024 年高考全景展示 1.【2024 年理数天津卷】已知函数,,其中 a>1.(I)求函数的单调区间;(II)若曲线在点处的切线与曲线在点处的切线平行,证明;(III)证明当时,存在直线 l,使 l 是曲线的切线,也是曲线的切线.2.【2024 年理北京卷】设函数=[].(Ⅰ)若曲线 y= f(x)在点(1,)处的切线与轴平行,求 a;(Ⅱ)若在 x=2 处取得微小值,求 a 的取值范围.3.【2024 年江苏卷】记分别为函数的导函数.若存在,满足且,则称为函数与的一个“S 点”.(1)证明:函数与不存在“S 点”;(2)若函数与存在“S 点”,求实数 a 的值;(3)已知函数,.对任意,推断是否存在,使函数与在区间内存在“S点”,并说明理由.4.【2024 年理新课标 I 卷】已知函数.(1)讨论的单调性;(2)若存在两个极值点,证明:.2024 年高考全景展示 1.【2024 课标 II,理 11】若是函数的极值点,则的微小值为( )A. B. C.2.【2024 浙江,7】函数 y=f(x)的导函数的图像如图所示,则函数 y=f(x)的图像可能是精品文档---下载后可任意编辑3.【2024 课标 II,理】已知函数,且。(1)求;(2)证明:存在唯一的极大值点,且。4.【2024 课标 3,理 21】已知函数.(1)若,求 a 的值;(2)设 m 为整数,且对于任意正整数 n,求 m 的最小值.5.【2024 浙江,20】(本题满分 15 分)已知函数 f(x)=(x–)().(Ⅰ)求 f(x)的导函数;(Ⅱ)求 f(x)在区间上的取值范围.6.【20...