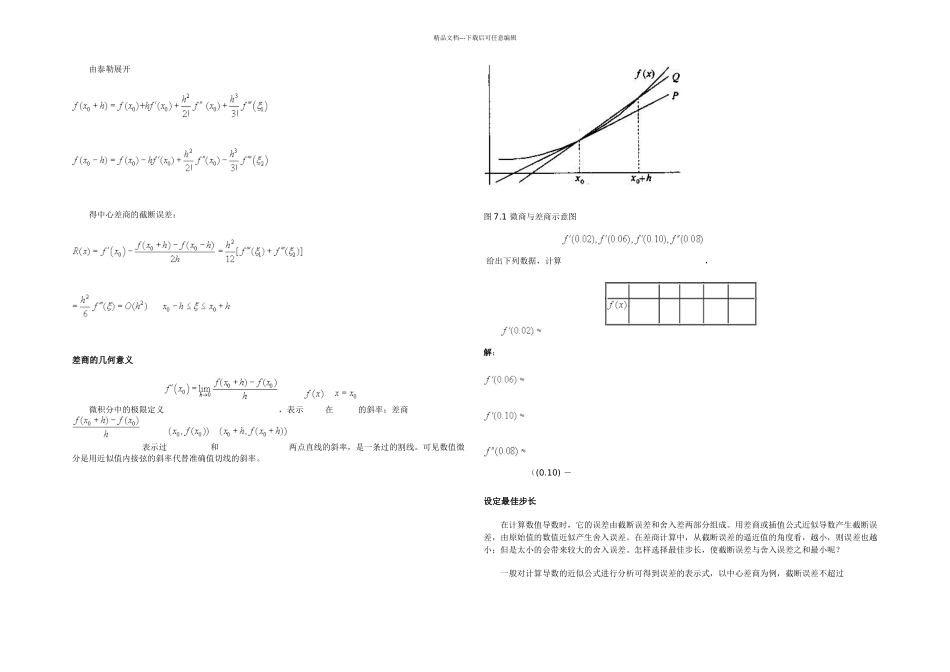
精品文档---下载后可任意编辑7.1 数值微分 差商与数值微分 当函数是以离散点列给出时,当函数的表达式过于复杂时,常用数值微分近似计算的导数。在微积分中,导数表示函数在某点上的瞬时变化率,它是平均变化率的极限;在几何上可解释为曲线的斜率;在物理上可解释为物体变化的速率。 以下是导数的三种定义形式: (7.1) 在微积分中,用差商的极限定义导数;在数值计算中返璞归真,导数取用差商(平均变化率)作为其近似值。 最简单的计算数值微分的方法是用函数的差商近似函数的导数,即取极限的近似值。下面是与式(7.1)相应的三种差商形式的数值微分公式以及相应的截断误差。向前差商 用向前差商(平均变化率)近似导数有: (7.2) 其中的位置在的前面,因此称为向前差商。同理可得向后差商、中心差商的定义。 由泰勒展开 得向前差商的截断误差: 向后差商 用向后差商近似导数有: (7.3) 与计算向前差商的方法类似,由泰勒展开得向后差商的截断误差:中心差商 用中心差商(平均变化率)近似导数有: (7.4)精品文档---下载后可任意编辑 由泰勒展开 得中心差商的截断误差: 差商的几何意义 微积分中的极限定义,表示在的斜率;差商表示过和两点直线的斜率,是一条过的割线。可见数值微分是用近似值内接弦的斜率代替准确值切线的斜率。图 7.1 微商与差商示意图 给出下列数据,计算,解:((0.10) -设定最佳步长 在计算数值导数时,它的误差由截断误差和舍入差两部分组成。用差商或插值公式近似导数产生截断误差,由原始值的数值近似产生舍入误差。在差商计算中,从截断误差的逼近值的角度看,越小,则误差也越小;但是太小的会带来较大的舍入误差。怎样选择最佳步长,使截断误差与舍入误差之和最小呢? 一般对计算导数的近似公式进行分析可得到误差的表示式,以中心差商为例,截断误差不超过精品文档---下载后可任意编辑 而舍入误差可用量估量(证明略),其中是函数的原始值的绝对误差限,总误差为 当时,总误差达到最小值,即 (*) 可以看到用误差的表达式确定步长,难度较大,难以实际操作。 通常用事后估量方法选取步长,例如,记为步长等于的差商计算公式,给定误差界,当时,就是合适的步长。 对函数,取不同的步长计算,观察误差变化规律,从而确定最佳步长。解:误差误差 表中数据显示,当步长从 0.10 减少到 0.03 时,数值微分误差的绝对值从 0.0048 减少到 0.0001,而随着的进一步减...