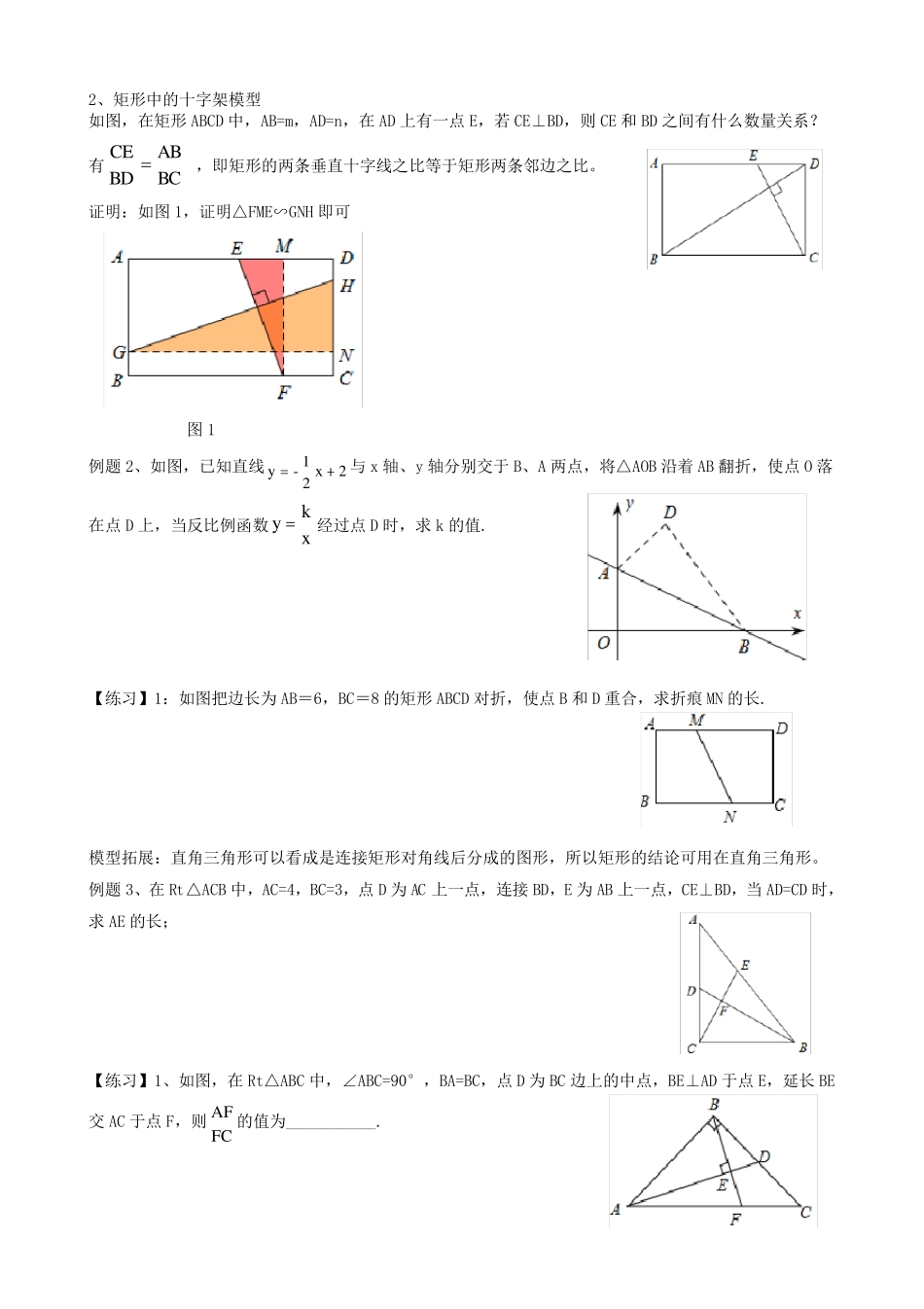
四边形中的十字架模型 引例:小学时就出现四边形中的十字架模型在四边形ABCD 中,AC⊥BD,AC=8,BD=10,求四边形ABCD 的面积。 1、正边形中的十字架模型 1、在正方形ABCD 中,BN⊥AM,则常见的结论有哪些? 2、在正方形ABCD 中,E、F、G、H 分别为AB、CD、BC、AD 边上的点,若EF⊥GH,上述结论仍然成立。 证明:作垂直。或记忆为:改斜归正,横平竖直。 结论:(1)△HNG≌△FME(2)GH=EF(垂等图) 注意:划线上的字很关键,否则,上述结论不成立。 从垂直可利用全等推导出相等,从相等是否可推导出垂直? 在正方形ABCD 中,E、F、G、H 分别为AB、CD、BC、AD 边上的点,若EF=GH,则EF 与GH 不一定垂直,请画出反例. 如下图,垂直只是相等时的一种情况,另一种,只需使得AH’=DH, BG’=CG’即可作出HG=H’G’ 通常情况下,可这样应用:由垂直可得相等,由相等可得垂直。 例题 1、如图,将边长为4 的正方形纸片 ABCD 折叠,使得点A 落在CD 的中点E 处,折痕为FG,点F 在AD 边,求折痕 FG 的长; 结论: △ADM≌△BAN AM=BN 2、矩形中的十字架模型 如图,在矩形ABCD 中,AB=m,AD=n,在AD 上有一点E,若CE⊥BD,则CE 和BD 之间有什么数量关系? 有 BCABBDCE ,即矩形的两条垂直十字线之比等于矩形两条邻边之比。 证明:如图1,证明△FME∽GNH 即可 图1 例题2、如图,已知直线2x21-y与x 轴、y 轴分别交于B、A 两点,将△AOB 沿着AB 翻折,使点O 落在点D 上,当反比例函数xky 经过点D 时,求k 的值. 【练习】1:如图把边长为AB=6,BC=8 的矩形ABCD 对折,使点B 和D 重合,求折痕MN 的长. 模型拓展:直角三角形可以看成是连接矩形对角线后分成的图形,所以矩形的结论可用在直角三角形。 例题3、在Rt△ACB 中,AC=4,BC=3,点D 为AC 上一点,连接BD,E 为AB 上一点,CE⊥BD,当AD=CD 时,求AE 的长; 【练习】1、如图,在Rt△ABC 中,∠ABC=90°,BA=BC,点D 为BC 边上的中点,BE⊥AD 于点E,延长BE交AC 于点F,则AFFC的值为___________. 3、平行四边形中的十字架模型 例4:如图,把边长为AB=2 2、BC=4 且∠B=45°的平行四边形ABCD 对折,使点 B 和 D 重合,求折痕MN 的长. 补成矩形就好了! BFDFBDMN,BD=102,DF=2,BF=6,所以 MN=3102 4、四边形中的十字架模型 例5:如图,若 BA=BC=6,DA=DC=8,∠BAD=90°.DE⊥CF,请求出 CFDE的值...