安徽工业大学工程力学练习册习题答案

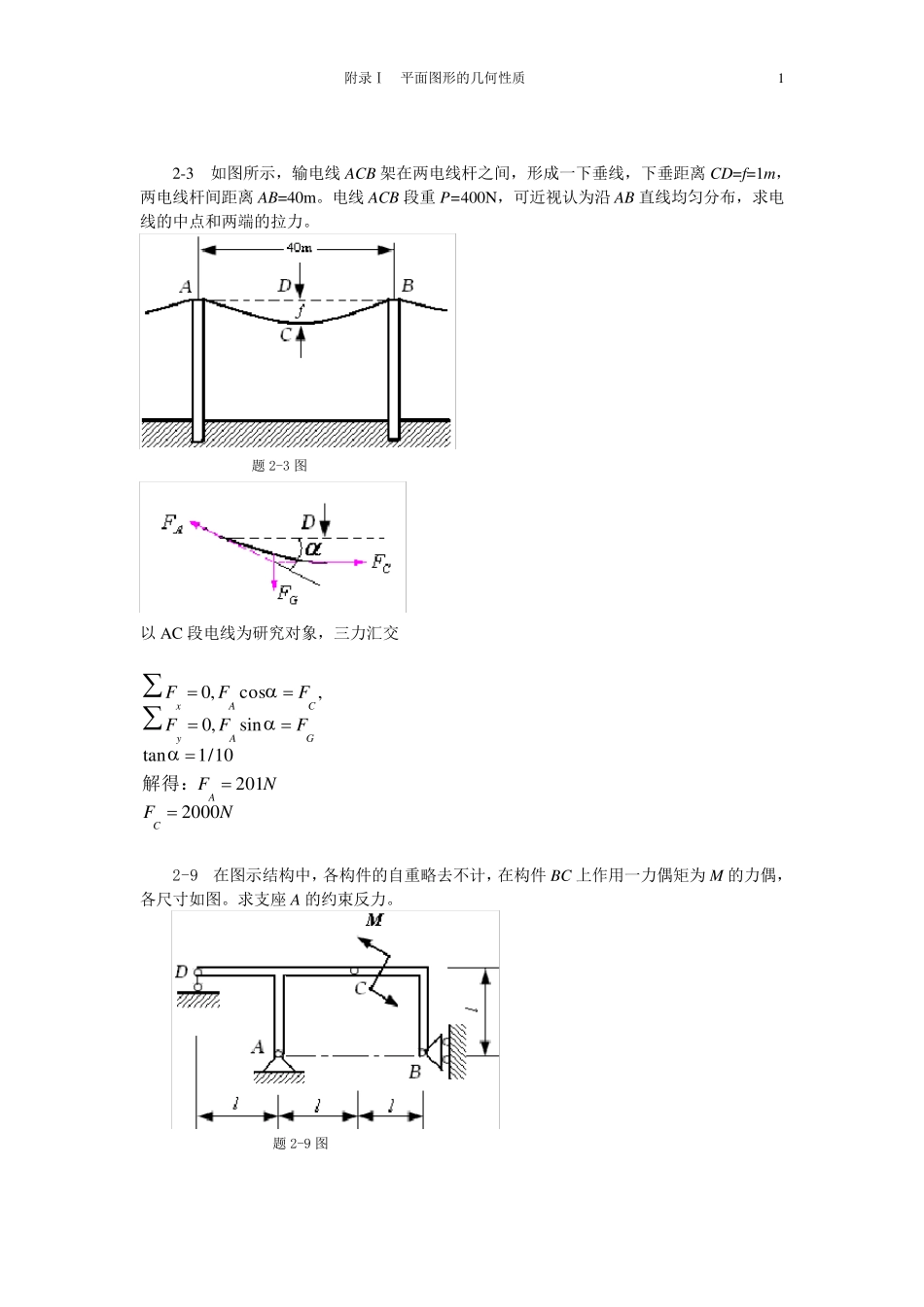
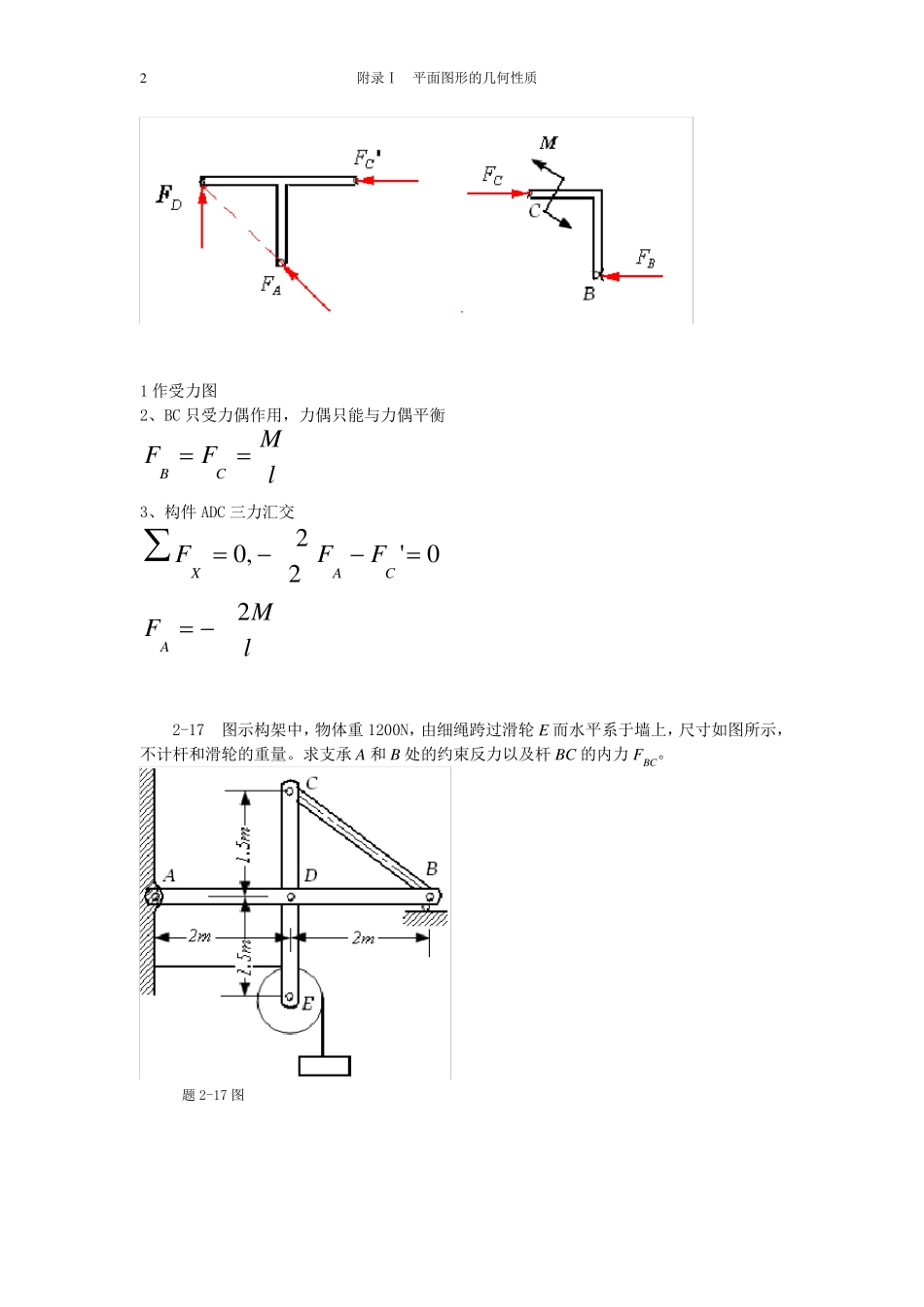
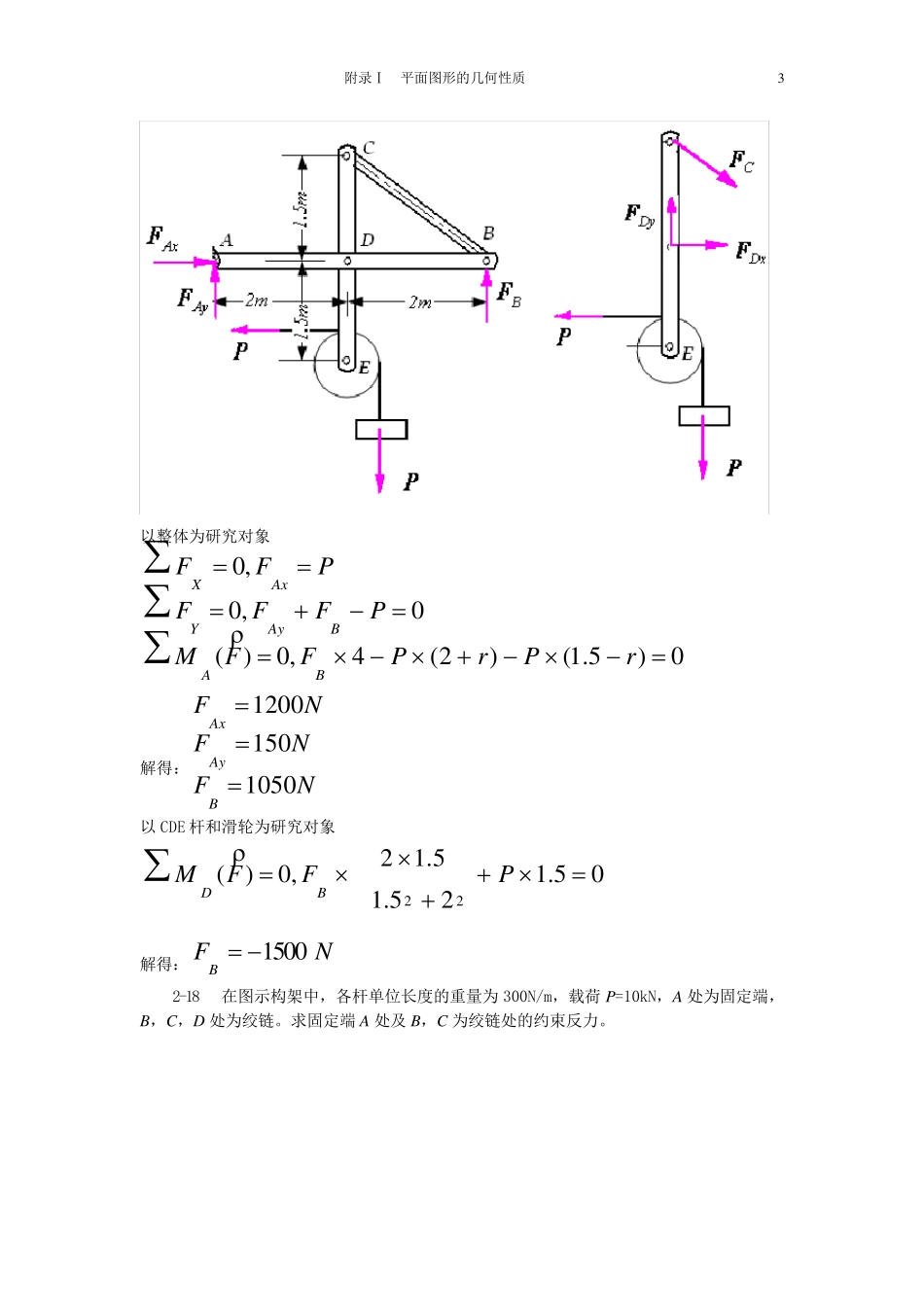
附录Ⅰ 平面图形的几何性质 1 2-3 如图所示，输电线 ACB 架在两电线杆之间，形成一下垂线，下垂距离 CD=f=1m，两电线杆间距离 AB=40m。电线 ACB 段重 P=400N，可近视认为沿 AB 直线均匀分布，求电线的中点和两端的拉力。 题 2-3 图 以 AC 段电线为研究对象，三力汇交 NFNFFFFFFFCAGAyCAx200020110/1tansin,0,cos,0解得： 2-9 在图示结构中，各构件的自重略去不计，在构件 BC 上作用一力偶矩为 M 的力偶，各尺寸如图。求支座 A 的约束反力。 题 2-9 图 2 附录Ⅰ 平面图形的几何性质 1 作受力图 2、BC 只受力偶作用，力偶只能与力偶平衡 lMFFCB 3、构件 ADC 三力汇交 lMFFFFACAX20'22,0 2-17 图示构架中，物体重 1200N，由细绳跨过滑轮 E 而水平系于墙上，尺寸如图所示，不计杆和滑轮的重量。求支承 A 和 B 处的约束反力以及杆 BC 的内力 FBC。 题 2-17 图 附录Ⅰ 平面图形的几何性质 3 以整体为研究对象 0)5.1()2(4,0)(0,0,0rPrPFFMPFFFPFFBABAyYAxX 解得：NFNFNFBAyAx1 0 5 01 5 01 2 0 0 以 CDE 杆和滑轮为研究对象 05.125.15.12,0)(22PFFMBD 解得：NFB1 5 0 0 2-18 在图示构架中，各杆单位长度的重量为 300N/m，载荷 P=10kN，A 处为固定端，B，C，D 处为绞链。求固定端 A 处及 B，C 为绞链处的约束反力。 4 附录Ⅰ 平面图形的几何性质 5 - 1 图示各梁，试利用剪力、弯矩与载荷集度间的关系画剪力图与弯矩图。 (a)Pl2l2lP q(b )2l2lq l 题 5-8图 附录Ⅰ 平面图形的几何性质 5 (c)q2l2lq q2q l2l2l(d) 题 5-8 图 (e)q4l2l4l DC(f)3lq lq3l3l 题 5-8 图 6 附录Ⅰ 平面图形的几何性质 a(g)aaqq2qa qaaaaqq(h ) 题 5-8 图 附录Ⅰ 平面图形的几何性质 7 6 - 1 求图示T 形铸铁梁的最大拉应力和最大压应力。 8 附录Ⅰ 平面图形的几何性质 ABC2m1m60qkN m中性轴48142542.59 10zIm 题 6-12 图 1.作梁的弯曲图 2.截面关于中性轴不对称，危险截面为最大正负弯矩两处 最大正弯矩处 最大负弯矩处： 综合得： MPaMPaCT3.311059.2104810875.165.921059.21014210875.1653315331MPaMPaCT5.1641059.21014210306.551059.21048103053325332...