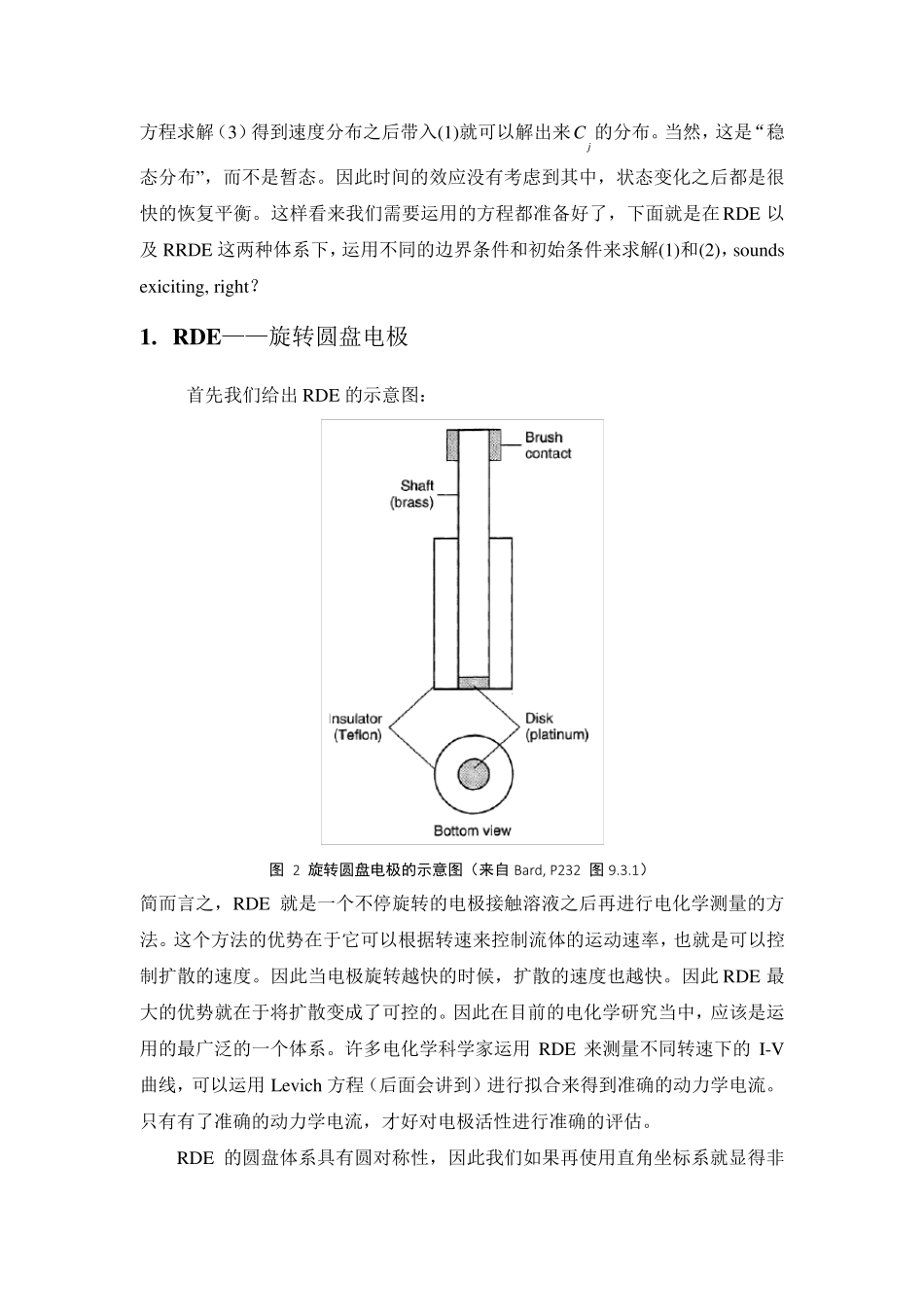
实验手段一——RDE 与RRDE 何政达1 在这篇文章中,我将详细的讨论有关旋转圆盘电极和旋转环盘电极相关的理论推导以及实验方法。并介绍由这两种方法得到的数据如何来进行数据分析。 旋转圆盘电极和旋转环盘电极最重要的相同点——就是它们都是在电极旋转的时候进行电化学测量。那么电极要是旋转起来,会对溶液造成什么样的影响呢?这就牵扯到了流体力学的相关知识。但是别急,我们将实际体系的物理方程一条一条的摆出来,然后看看应该如何去做。 首先我们要介绍的方程是“对流-扩散方程” 。由于物质在溶液中的流动形式只有可能为三种— — 对流、扩散、迁移。因此对每一项的贡献相加后就可以得到物质流动的方程式: jjjjjjjconvectiondiffusionmigrationz FJDCD CC vRT (1) jJ 代表了 j 物种的流量,jC 则为 j 物种的浓度。jD 为 j 物种的扩散系数,v 代表流体的流动速度, 代表在流体中的电势。等式右边第一项代表扩散、第二项代表迁移、第三项代表对流。我们有了jJ 之后就可以求出来jC ,根据Fick 第二定律: jjCJt (2) 因此只要将(1)带入(2)中我们就可以得到关于jC 的表达式。但是先别高兴,有没有发现在(1)中有两个未知参数? ,v。这两个参数我们如何得到?那么光用物质的流动方程就不够了。因此需要在电极要求的条件下,去求解流体力学当中最恐怖的一个微分方程— — Navier-Stokes 方程。它的具体形式为: 2SSdvdPvfdt (3) 其中Sd 为流体的密度。P 为流体的压力场,S为流体的黏度。f 为重力作用在 1 Email: jameshzd@mail.ustc.edu.cn QQ: 3231491610 液体单位体积上的力。但是看到这个方程之后,第一反应是——“我去!这么复杂的方程能解出来么”。。。但是别急,我们先介绍一个在流体力学中大家已经公认的事实,然后来简化 Nav ier-Stokes 方程:在流体力学中,流体的运用分为层流和湍流两种,它们的示意图如下: 图 1 层流和湍流的示意图(来自 Bard, P232 图9.2.1) 其中左边是层流,因为它的流动“平滑且稳定,就像各个层(层状)液体都具有稳定和特有的速度那样”2。右边的是湍流,“当流动引起的不稳定和紊乱运动时,此时在一个具体的方向上的净流动只有平均值”。湍流非常的复杂,到目前为止还没有很好的数学描述,被认为是 21 世纪重大数学难题。当然前面 Nav ier-Stokes方程的精确求解也是 21 世纪的一...