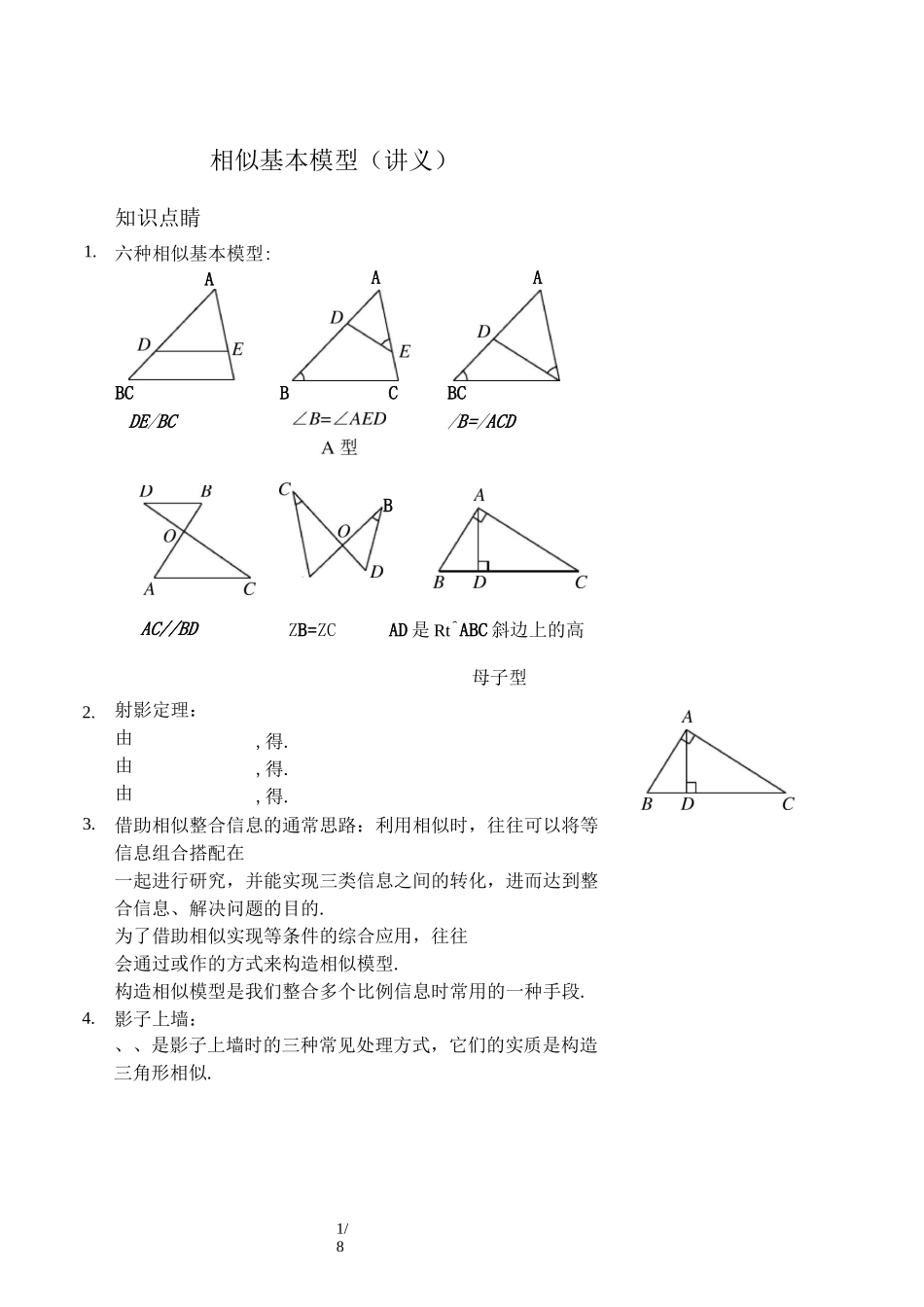
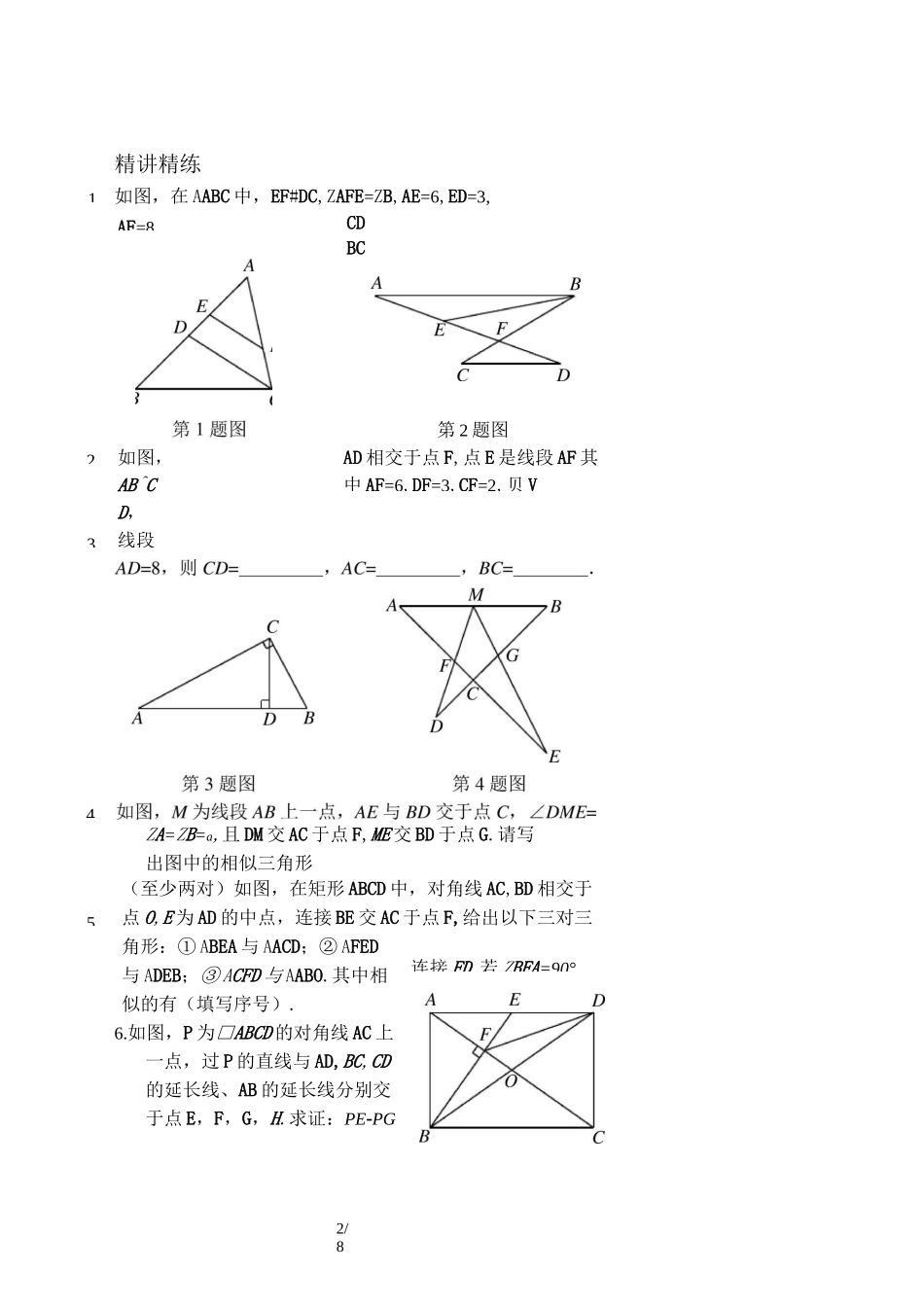
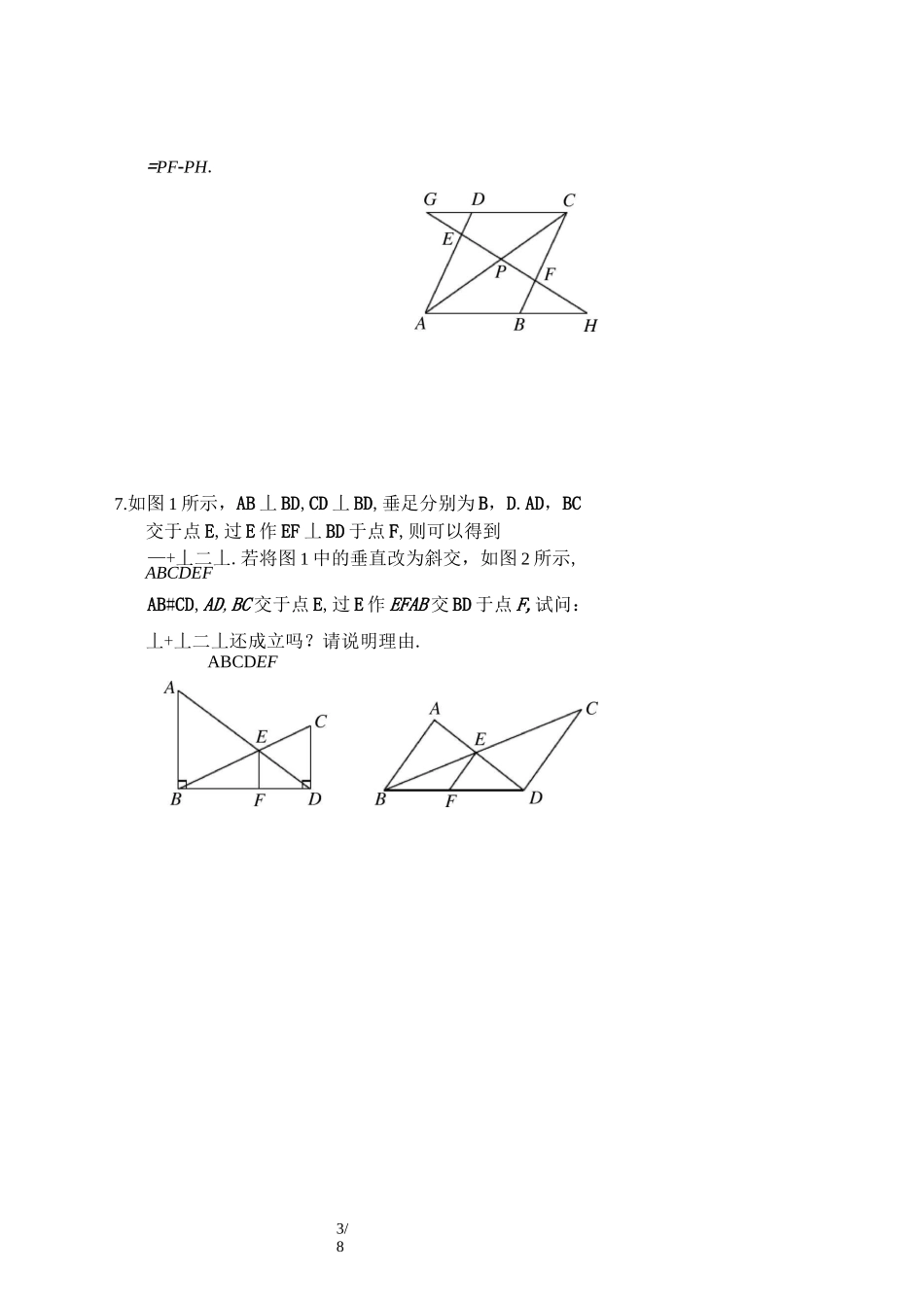
1/8相似基本模型(讲义)知识点睛1.AACB六种相似基本模型:ABC/B=/ACDBCDE/BCAC//BDB2.射影定理:由由由3.4.ZB=ZC,得.,得.,得.AD 是 Rt^ABC 斜边上的高母子型借助相似整合信息的通常思路:利用相似时,往往可以将等信息组合搭配在一起进行研究,并能实现三类信息之间的转化,进而达到整合信息、解决问题的目的.为了借助相似实现等条件的综合应用,往往会通过或作的方式来构造相似模型.构造相似模型是我们整合多个比例信息时常用的一种手段.影子上墙:、、是影子上墙时的三种常见处理方式,它们的实质是构造三角形相似.1AF=8234第 2 题图AD 相交于点 F,点 E 是线段 AF 其中 AF=6,DF=3,CF=2,贝 V如图,AB^CD,线段52/8精讲精练如图,在 AABC 中,EF#DC,ZAFE=ZB,AE=6,ED=3,CDBCZA=ZB=a,且 DM 交 AC 于点 F,ME 交 BD 于点 G.请写出图中的相似三角形(至少两对)如图,在矩形 ABCD 中,对角线 AC,BD 相交于点 O,E 为 AD 的中点,连接 BE 交 AC 于点 F,给出以下三对三角形:① ABEA 与 AACD;② AFED与 ADEB;③ ACFD 与 AABO.其中相似的有(填写序号).6.如图,P 为□ABCD 的对角线 AC 上一点,过 P 的直线与 AD,BC,CD的延长线、AB 的延长线分别交于点 E,F,G,H.求证:PE-PG连接 FD.若 ZBFA=90°,3/8=PF-PH.7.如图 1 所示,AB 丄 BD,CD 丄 BD,垂足分别为 B,D.AD,BC交于点 E,过 E 作 EF 丄 BD 于点 F,则可以得到—+丄二丄.若将图 1 中的垂直改为斜交,如图 2 所示,ABCDEFAB#CD,AD,BC 交于点 E,过 E 作 EFAB 交 BD 于点 F,试问:丄+丄二丄还成立吗?请说明理由.ABCDEF9如图,直线 l]〃12,若 AFFB=23,BCCD=21,则 CEAE=.l14/88.如图,在△ABC 中,CD 丄 AB 于点 D,正方形 EFGH 的四个顶点都在△ABC 的边上•求证:丄+丄=丄•ABCDEF如图,在△ABC 中,AE=CE,BC=CD.求证:ED=3EF.D5/811.如图,直线 l 与△ABC 三边所在直线分别交于点 E,F,且BFAF=23,EFFD=54,求 ADCD 的值.C.(7+誇)米6/8D.(14+2J3)米12. 数学兴趣小组想测量一棵树的高度.在阳光下,一名同学测得一根长为 1 米的竹竿的影长为 0.8 米,同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),这部分影长为 1.2 米,落在地面上的影长为 2.4 米,则树高为.第 12 题图第 13 题图13. 小阳发现电线杆 AB 的影子落在...