材料力学专题一梁的内力和内力图

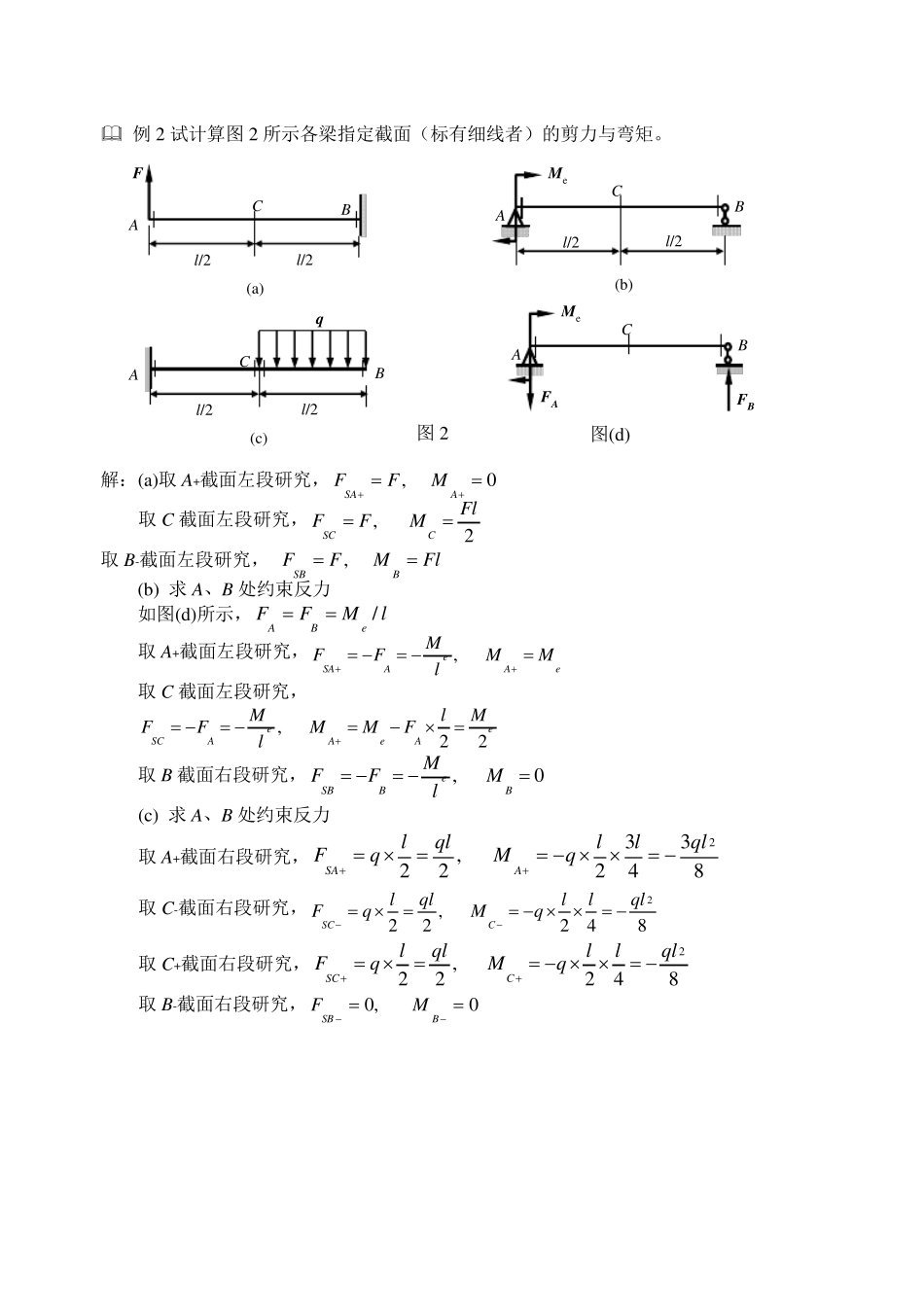
专题一 梁的内力和内力图  例1 求图1(a)所示梁截面 A、C 的剪力和弯矩。 解：1）求反力 kN5AF， kN4BF 2）求A 左截面的内力，如图(a)所示。 0iY， 0左SApFF，kN3左SAF 0OM，02左ApMF， mkN6左AM 3）求A 右截面的内力，如图(b)所示。 0iY，0ASApFFF左，kN2左SAF 0OM，02右ApMF， mkN6右AM 4）求C 左截面的内力，如图(c)所示。 0iY，02左SCPAFqFF， 0左SCF 0OM，01224左CApMqFF，左CMmkN4 5）求C 右截面的内力，如图(d)所示。 0iY，02右SCPAFqFF，0235右SCF 0OM，012241右CApMMqFF，右CMmkN6 【小结】①求 指 定 截 面 上 的 内 力 时 ， 既 可 取 梁 的 左 段 为 脱 离 体 ， 也 可 取 右 段 为 脱 离 体 ，两 者 计 算 结 果 一 致 。一 般取 外力 比较简单的 一 段 进行分析。②在解题时 ， 通常假设截 面 上把内 力 为 正， 若最后计 算 结 果 是正， 则表示假设的 内 力 方向（转向）与实际是相同的 ， 否则是相反的 。③该题也 可 以不画受力 图， 不写平衡方程而由前面 的 结 论直接求 得结 果 。 图1 (a) (b) (c) (d) (e)  例2 试计算图2 所示各梁指定截面（标有细线者）的剪力与弯矩。 解：(a)取A+截面左段研究，, 0SAAFFM 取C 截面左段研究， , 2SCCFlFFM 取B-截面左段研究， , SBBFFMFl (b) 求A、B 处约束反力 如图(d)所示，lMFFeBA/ 取A+截面左段研究，, eSAAAeMFFMMl   取C 截面左段研究， , 22eeSCAAeAMMlFFMMFl   取B 截面右段研究，, 0eSBBBMFFMl   (c) 求A、B 处约束反力 取A+截面右段研究，233, 22248SAAlq lllq lFqMq    取C-截面右段研究，2, 22248SCClq lllq lFqMq    取C+截面右段研究，2, 22248SCClq lllq lFqMq    取B-截面右段研究， 0, 0SBBFM 图2 A Me (b) B C l/2 l/2 A C B l/2 l/2 (a) F q A C B l/2 l/2 (c) FA A Me B C FB 图(d)  例3 试写出图3 所示梁的内力方程，并画出剪...