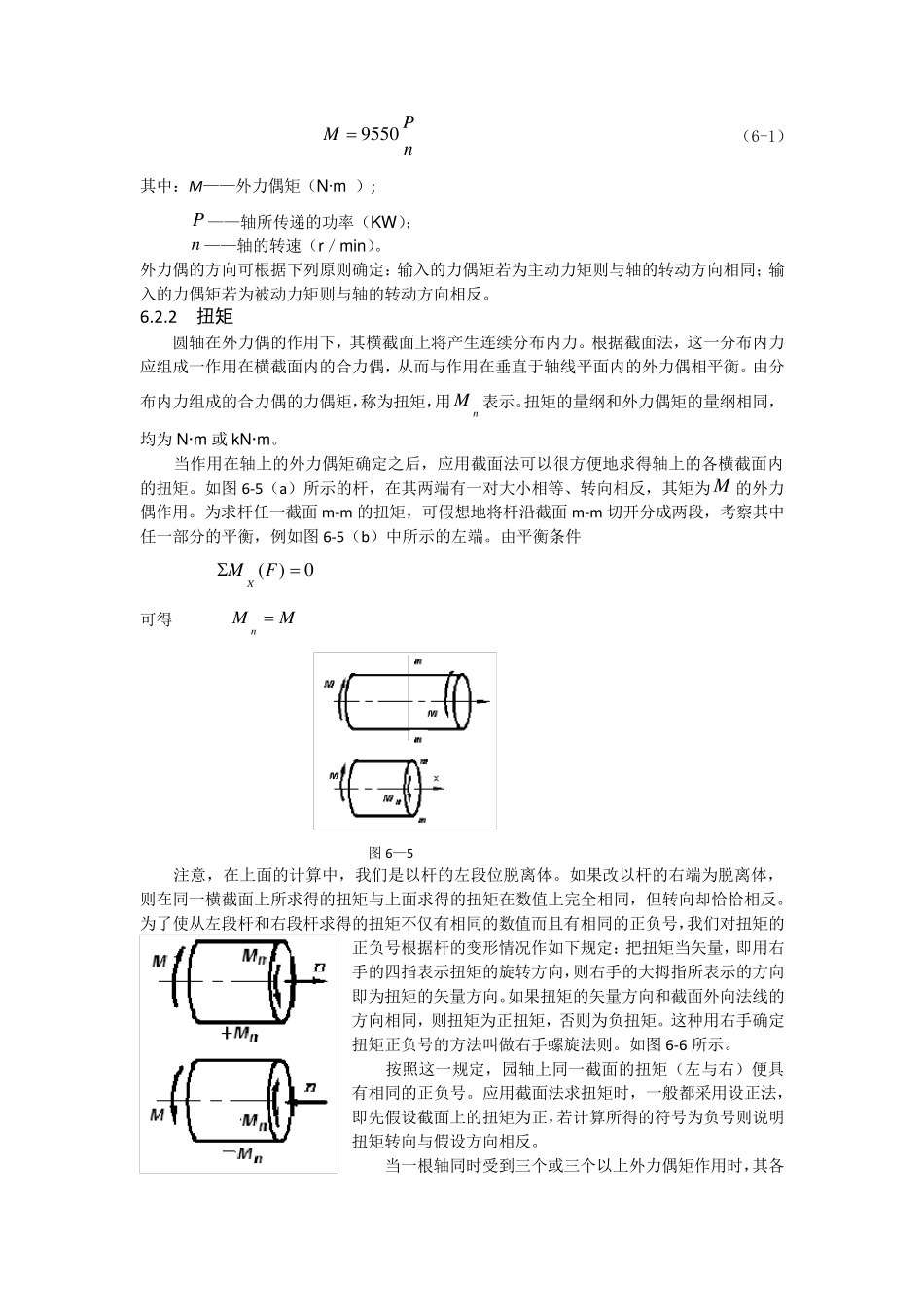
材料力学 扭转 6 .1 扭 转 的 概 念 扭转是杆件变形的一种基本形式。在工程实际中以扭转为主要变形的杆件也是比较多的,例如图6-1 所示汽车方向盘的操纵杆,两端分别受到驾驶员作用于方向盘上的外力偶和转向器的反力偶的作用;图6-2 所示为水轮机与发电机的连接主轴,两端分别受到由水作用于叶片的主动力偶和发电机的反力偶的作用;图6-3 所示为机器中的传动轴,它也同样受主动力偶和反力偶的作用,使轴发生扭转变形。 图6—1 图6—2 图6—3 这些实例的共同特点是:在杆件的两端作用两个大小相等、方向相反、且作用平面与杆件轴线垂直的力偶,使杆件的任意两个截面都发生绕杆件轴线的相对转动。这种形式的变形称为扭转变形(见图6-4)。以扭转变形为主的直杆件称为轴。若杆件的截面为圆形的轴称为圆轴。 图6—4 6 .2 扭 矩 和扭 矩 图 6.2.1 外力偶矩 作用在轴上的外力偶矩,可以通过将外力向轴线简化得到,但是,在多数情况下,则是通过轴所传递的功率和轴的转速求得。它们的关系式为 nPM9 5 5 0 (6-1) 其中:M ——外力偶矩(N·m ); P ——轴所传递的功率(KW); n——轴的转速(r/min)。 外力偶的方向可根据下列原则确定:输入的力偶矩若为主动力矩则与轴的转动方向相同;输入的力偶矩若为被动力矩则与轴的转动方向相反。 6.2.2 扭矩 圆轴在外力偶的作用下,其横截面上将产生连续分布内力。根据截面法,这一分布内力应组成一作用在横截面内的合力偶,从而与作用在垂直于轴线平面内的外力偶相平衡。由分布内力组成的合力偶的力偶矩,称为扭矩,用nM 表示。扭矩的量纲和外力偶矩的量纲相同,均为 N·m 或 kN·m。 当作用在轴上的外力偶矩确定之后,应用截面法可以很方便地求得轴上的各横截面内的扭矩。如图 6-5(a)所示的杆,在其两端有一对大小相等、转向相反,其矩为 M 的外力偶作用。为求杆任一截面 m -m 的扭矩,可假想地将杆沿截面 m -m 切开分成两段,考察其中任一部分的平衡,例如图 6-5(b)中所示的左端。由平衡条件 0)(FMX 可得 MMn 图 6—5 注意,在上面的计算中,我们是以杆的左段位脱离体。如果改以杆的右端为脱离体,则在同一横截面上所求得的扭矩与上面求得的扭矩在数值上完全相同,但转向却恰恰相反。为了使从左段杆和右段杆求得的扭矩不仅有相同的数值而且有相同的正负号,我们对扭矩的正负号根据杆的变形情况作如下规定:把扭矩当矢量,即用...