材料力学答案第三版单辉祖

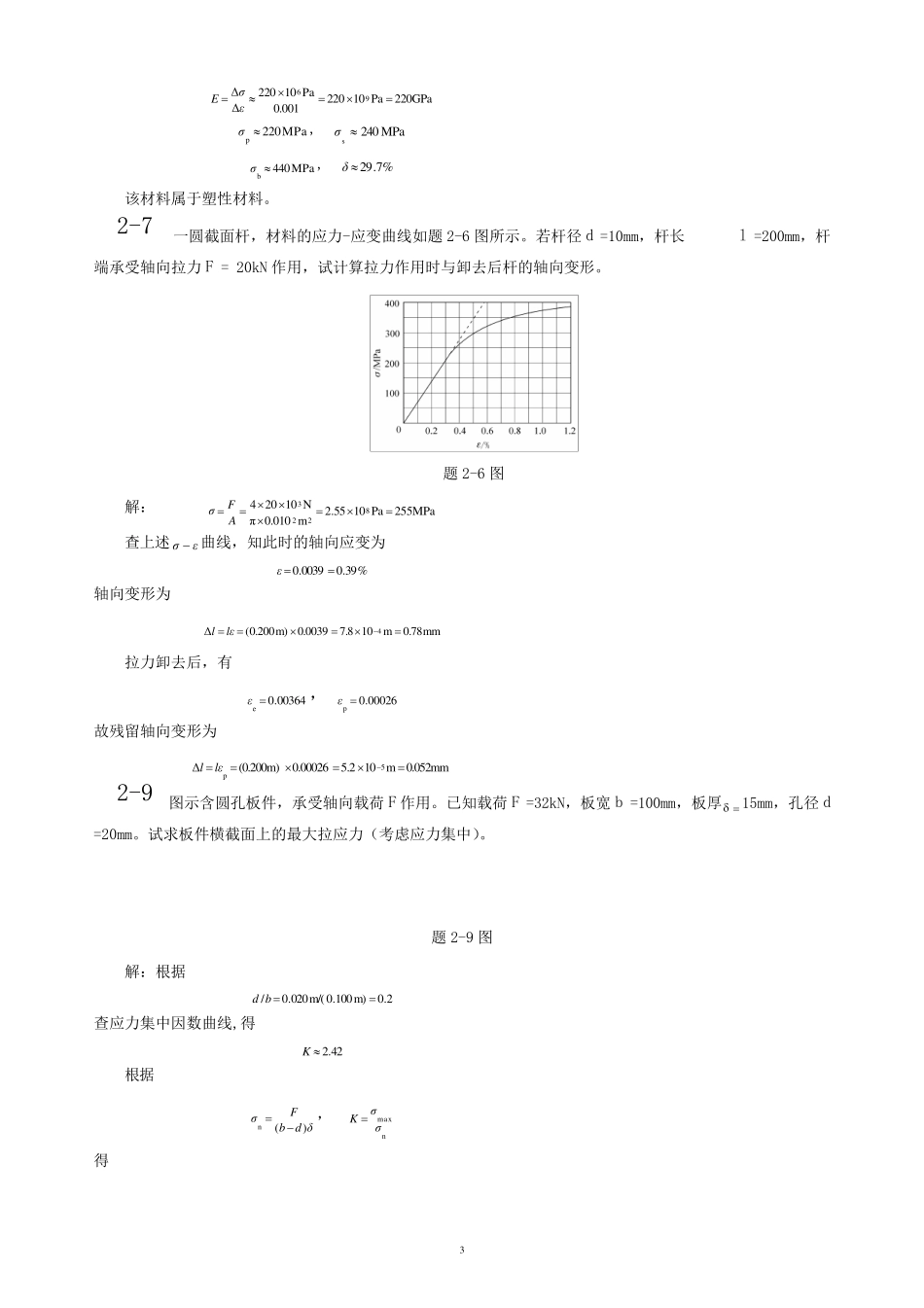
1 第二章 轴向拉压应力与材料的力学性能 2-1 试画图示各杆的轴力图。 题 2-1 图 解：各杆的轴力图如图2-1 所示。 图2-1 2-2 试画图示各杆的轴力图，并指出轴力的最大值。图a 与b 所示分布载荷均沿杆轴均匀分布，集度为q。 题 2-2 图 (a)解：由图2-2a(1)可知， qxqaxF2)(N 轴力图如图2-2a(2)所示， qaF2max,N 图2-2a (b)解：由图2-2b(2)可知， qaF R 2 qaFxFR1N)( 22R2N2)()(qxqaaxqFxF 轴力图如图2-2b(2)所示， qaFmaxN, 图2-2b 2-3 图示轴向受拉等截面杆，横截面面积A=500mm2，载荷F=50kN。试求图示斜截面m-m 上的正应力与切应力，以及杆内的最大正应力与最大切应力。 题2-3 图 解：该拉杆横截面上的正应力为 100MPaPa1000.1m10500N10508263－AFσ 斜截面m-m 的方位角，50α故有 MPa3.41)50(cosMPa100cos22ασσ MPa2.49)100sin(MPa502sin2αστα 杆内的最大正应力与最大切应力分别为 MPa100max σσ MPa502max στ 2-5 某材料的应力-应变曲线如图所示，图中还同时画出了低应变区的详图。试确定材料的弹性模量E、比例极限p 、屈服极限s 、强度极限b 与伸长率，并判断该材料属于何种类型（塑性或脆性材料）。 题2-5 解：由题图可以近似确定所求各量。 3 220GPaPa102200.001Pa10220ΔΔ96εσE MPa220p σ, MPa240s σ MPa440b σ, %7.29δ 该材料属于塑性材料。 2-7 一圆截面杆，材料的应力-应变曲线如题 2-6 图所示。若杆径 d =10mm，杆长 l =200mm，杆端承受轴向拉力 F = 20kN 作用，试计算拉力作用时与卸去后杆的轴向变形。 题 2-6 图 解： 255MPaPa1055.2m0.010πN102048223 AFσ 查上述εσ  曲线，知此时的轴向应变为 %39.00039.0ε 轴向变形为 mm780m108700390m)2000(Δ4....lεl 拉力卸去后，有 00364.0e ε， 00026.0p ε 故残留轴向变形为 0.052mmm105.2000260(0.200m)Δ5p.lεl 2-9 图示含圆孔板件，承受轴向载荷 F 作用。已知载荷 F =32kN，板宽 b =100mm，板厚 15mm，孔径 d =20mm。试求板件横截面上的最大拉应力（考虑应力集中）。 题 2-9 图 解：根据 2.0m)100.0m/(020.0/bd 查应力集中因数曲线,得 42.2K 根据 δdbFσ)...