极大似然估计及其性质

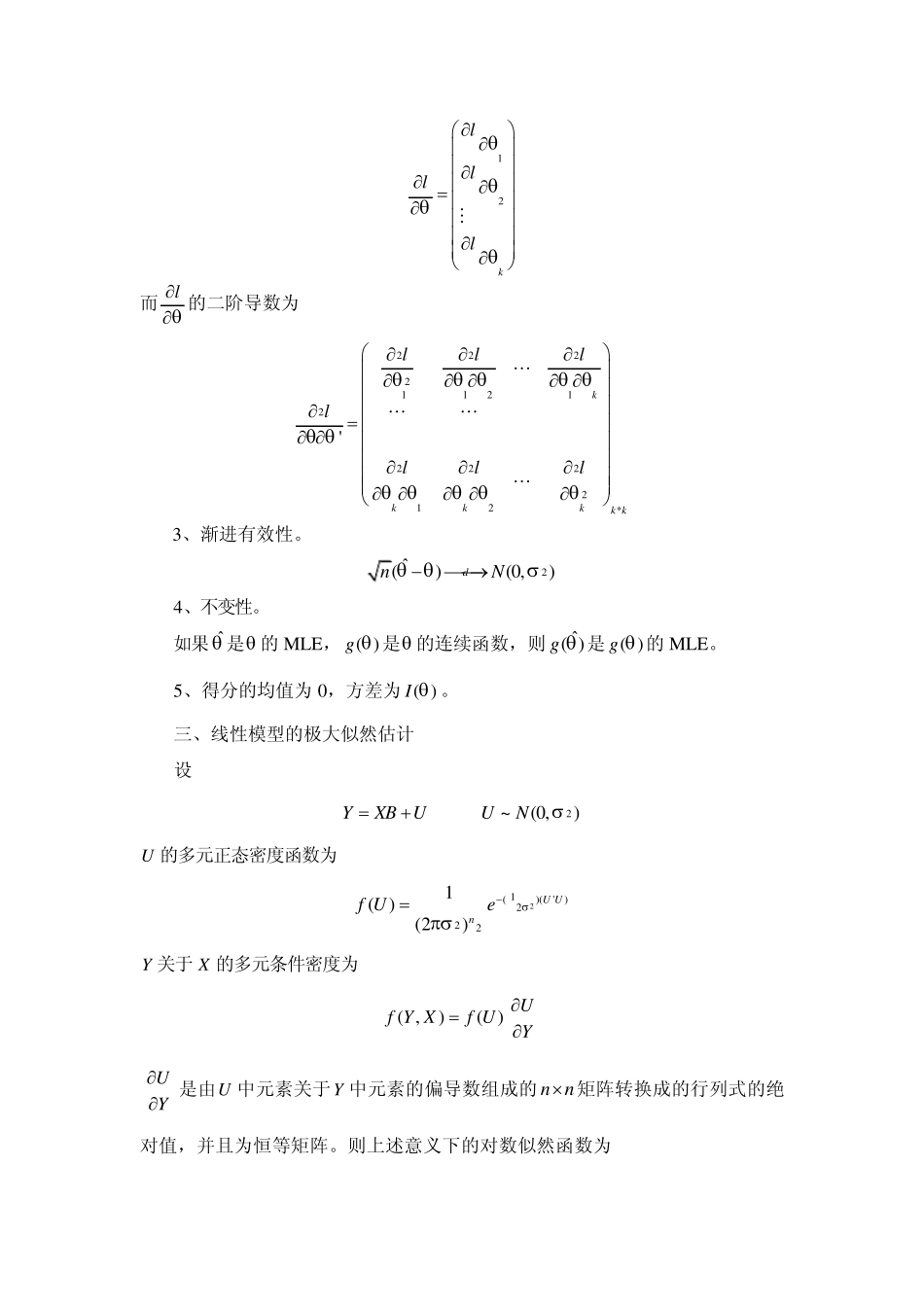
极大似然估计及其性质 一、极大似然估计 设联合密度函数为 12( ; ),'()kf Y  则似然函数为 似然函数( ; )( ; )LYf Y 为使关于 的似然函数最大化，求 的一个估计ˆ ，使获得的已观测到的样本值的概率自大化，即最大似然估计量（MLE）。 定义对数似然函数为 lnlL 则 ll LL 最大化 l 的 ˆ 值也会最大化 L ，l 对 的导数 ( ; )sY称作得分，将得分定义为 0，即可解出（MLE） ˆ ，即 ( ; )0lsY 二、MLE 的性质 1、一致性。 ˆlim( )P 2、渐进正态性。 1ˆ ~( ,( ))NI 式中 ( )I  为信息矩阵 2( )'lllIEE    当 是一个k 维向量时， l表示k 个偏导数组成的列向量，即 12kllll  而l的二阶导数为 222211212222212*'kkkkk klllllll          3、渐进有效性。 2ˆ()(0,)dnN 4、不变性。 如果 ˆ 是 的MLE， ( )g  是 的连续函数，则ˆ( )g  是 ( )g  的MLE。 5、得分的均值为0，方差为( )I  。 三、线性模型的极大似然估计 设 2~ (0,)YXBUUN U 的多元正态密度函数为 21()(')2221( )(2)U Unf Ue Y 关于 X 的多元条件密度为 ( ,)( )Uf Y Xf UY UY是由U 中元素关于Y 中元素的偏导数组成的nn 矩阵转换成的行列式的绝对值，并且为恒等矩阵。则上述意义下的对数似然函数为 22221ln( (| )ln()ln 2ln'2221ln 2ln()'()222nnlf Y XUU UnnYXBYXB   求2,B  的偏导数 22241 ('')21 ()'()22lX YX XBBlnYXBYXB    令其为零，可解出极大似然估计 12ˆ(')'ˆˆ()'()BX XX YYXBYXBn 并且，ˆ( )E BB，但2ˆ 不是2 的无偏估计，由于22(')()E U UEun（基于同方差性），因此，求二阶导数为 222222242222246224'',()''',()0,( (')0)',9()()2()2lX XlX XEB BB ...